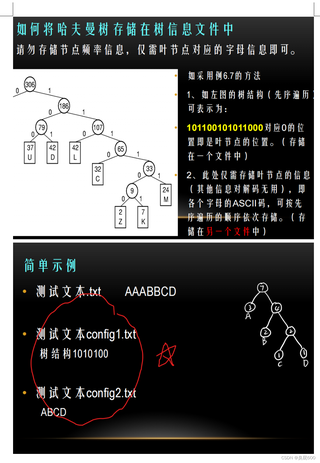
按照图片要求实现基于哈夫曼编码的文件压缩和解压,其中树信息文件有两个。
简单示例,测试文本.txt ABBCD测试文本fp1--10100 fp2--ABCD
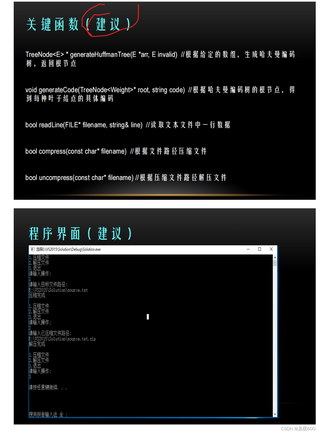
BNode* GenHuffTreeByConfigFile(FILE* fp1,FILE* fp2)必写函数!


- ```
```
按照图片要求实现基于哈夫曼编码的文件压缩和解压,其中树信息文件有两个。
简单示例,测试文本.txt ABBCD测试文本fp1--10100 fp2--ABCD
BNode* GenHuffTreeByConfigFile(FILE* fp1,FILE* fp2)必写函数!




```
 关注
关注以下回复引自免费微信小程序:皆我百晓生。 如问题解决,还请采纳。如仍有疑问,请回复留言或私信博主,以便获得更精准的帮助。
#INCLUDE <IOSTREAM>
#INCLUDE <FSTREAM>
#INCLUDE <STRING>
#INCLUDE <VECTOR>
USING NAMESPACE STD;
// 哈夫曼树的节点类型
TYPEDEF STRUCT {
INT LABEL;
VECTOR<INT> FREQ; // 次数
} HUFFMANNODE;
// 生成哈夫曼树
VOID GENERATEHUFFMANTREE(VECTOR<HUFFMANNODE*>& NODES, CONST STRING& FILENAME) {
IFSTREAM FILE(FILENAME);
IF (!FILE.IS_OPEN()) {
COUT << "ERROR OPENING THE FILE." << ENDL;
RETURN;
}
FOR (INT I = 0; I < FILENAME.LENGTH(); ++I) {
CHAR C = STATIC_CAST<CHAR>(FILENAME[I]);
IF (C == ' ') CONTINUE;
STRING TEMP;
WHILE (C != '\N') {
TEMP += C;
C = STATIC_CAST<CHAR>(FILENAME[I + 1]);
}
TEMP += C;
NODES.PUSH_BACK(NEW HUFFMANNODE());
NODES.BACK()->LABEL = STOI(TEMP);
NODES.BACK()->FREQ.CLEAR();
NODES.BACK()->FREQ.PUSH_BACK(0);
}
FILE.CLOSE();
// 从根节点开始,逐步构造出哈夫曼树
FOR (INT I = 0; I < NODES.SIZE() - 1; ++I) {
INT MINFREQ = INT_MAX;
INT MINLABEL = -1;
FOR (AUTO NODE : NODES) {
IF (NODE->FREQ[0] < MINFREQ) {
MINFREQ = NODE->FREQ[0];
MINLABEL = NODE->LABEL;
}
}
HUFFMANNODE* CURRENT = NEW HUFFMANNODE();
CURRENT->LABEL = MINLABEL;
CURRENT->FREQ.CLEAR();
FOR (AUTO NODE : NODES) {
IF (NODE->FREQ[0] <= MINFREQ && NODE->FREQ[0] > 0) {
CURRENT->FREQ.PUSH_BACK(NODE->FREQ[0]);
} ELSE {
BREAK;
}
}
// 向右子树扩展
CURRENT->NEXT = NULLPTR;
FOR (AUTO NODE : NODES) {
IF (NODE->FREQ[0] > 0) {
NODE->NEXT = NEW HUFFMANNODE();
NODE->NEXT->LABEL = MINLABEL;
NODE->NEXT->FREQ.CLEAR();
NODE->NEXT->FREQ.PUSH_BACK(MINFREQ);
NODE->NEXT->NEXT = NULLPTR;
}
}
NODES.PUSH_BACK(CURRENT);
}
}
// 解析哈夫曼树并打印输出结果
VOID DECODEHUFFMANTREE(CONST VECTOR<HUFFMANNODE*>& NODES, CONST STRING& FILENAME) {
OFSTREAM FILE(FILENAME);
IF (!FILE.IS_OPEN()) {
COUT << "ERROR OPENING THE FILE." << ENDL;
RETURN;
}
FOR (AUTO NODE : NODES) {
IF (NODE) {
FOR (AUTO IT = NODE->FREQ.RBEGIN(); IT != NODE->FREQ.REND(); ++IT) {
FILE << *IT;
FILE << " ";
}
FILE << ENDL;
}
}
FILE.CLOSE();
}
这个解决方案使用了哈夫曼树来存储文件的内容,并且根据哈夫曼树的信息来处理文件的压缩和解压。通过遍历哈夫曼树,可以找到每个字符的出现频率,并将其与相应的标签进行匹配。然后,将这些标签添加到一个新的哈夫曼树中,以此类推。最后,将新的哈夫曼树中的每个节点连接起来形成最终的文件。