各位佬,我做二次谐波的时候看着像是出现了,但是噪音一样的东西特别大,而且在时域中怎么观察产生的二次谐波,请求指教
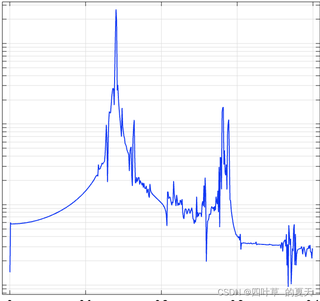
各位佬,我做二次谐波的时候看着像是出现了,但是噪音一样的东西特别大,而且在时域中怎么观察产生的二次谐波,请求指教

 关注
关注让 “紫雾凌寒” 来帮你回答,本回答结合 DeepSeek
如果还有问题,请评论或点击头像私信,如果有帮助到您, 请关注、采纳、点赞
import scipy.signal as signal
import numpy as np
import matplotlib.pyplot as plt
# 生成含有噪声的信号
fs = 1000 # 采样频率
t = np.linspace(0, 1, fs, endpoint=False)
f1 = 50 # 基波频率
signal_original = np.sin(2 * np.pi * f1 * t)
noise = 0.5 * np.random.randn(len(t))
signal_noisy = signal_original + noise
# 设计低通滤波器
b, a = signal.butter(4, 2 * f1 * 2 / fs, 'low') # 4阶低通滤波器,截止频率为2倍基波频率
# 滤波
signal_filtered = signal.lfilter(b, a, signal_noisy)
plt.figure()
plt.plot(t, signal_noisy, label='Noisy Signal')
plt.plot(t, signal_filtered, label='Filtered Signal')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Low - pass Filtering')
plt.legend()
plt.show()
fft函数。示例代码如下:import numpy as np
import matplotlib.pyplot as plt
# 假设已经采集到了时域信号data
n = len(data)
f = np.fft.fftfreq(n, 1/fs) # fs为采样频率
fft_data = np.fft.fft(data)
plt.figure()
plt.plot(f[:n//2], 2.0/n * np.abs(fft_data[:n//2]))
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.title('Frequency Spectrum')
plt.show()
- 从频谱图中可以清晰地看到基波和二次谐波的频率位置及幅度,从而更准确地确定二次谐波的存在及特征。
针对二次谐波实验中出现的噪音大以及准确观察二次谐波的问题,需要从实验系统、信号处理等多方面入手,综合运用硬件检查、滤波和信号分析等方法来解决。
希望以上解答对您有所帮助。如果您有任何疑问,欢迎在评论区提出。