为什么这个老递归不对呀我破防了

Question

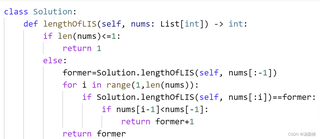
题目是：给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

Answer 1

问题分析

你的递归代码试图解决“最长严格递增子序列（LIS）”问题，但存在以下问题：

1. 语法错误：
   • if 和 else 的缩进不正确。
   • List[int] 需要从 typing 导入。
   • 递归调用时直接使用 Solution.lengthOfLIS(self, ...) 是不规范的，应该用 self.lengthOfLIS(...)。
2. 逻辑错误：
   • 当 len(nums) <= 1 时，直接返回 1 是错误的。例如，nums = [] 应该返回 0，nums = [5] 应该返回 1。
   • 递归逻辑无法正确计算 LIS 的长度。例如，对于 nums = [1, 2, 3]，你的代码无法正确返回 3。

修复后的递归代码

以下是修复后的递归代码，但需要注意：递归解法的时间复杂度是指数级的（O(2^n)），对于较大的输入会超时。实际中应使用动态规划（O(n²)）或贪心+二分查找（O(n log n)）。

from typing import List

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        if len(nums) == 1:
            return 1
        
        # 递归计算前 n-1 个元素的 LIS 长度
        former = self.lengthOfLIS(nums[:-1])
        
        # 检查是否可以将 nums[-1] 添加到某个子序列中
        max_len = former
        for i in range(len(nums) - 1):
            if nums[i] < nums[-1]:
                # 递归计算 nums[:i+1] 的 LIS 长度 + 1（包含 nums[-1]）
                current_len = self.lengthOfLIS(nums[:i + 1]) + 1
                if current_len > max_len:
                    max_len = current_len
        
        return max(former, max_len)

递归逻辑解释

1. 基本情况：
   • 如果 nums 为空，返回 0。
   • 如果 nums 只有一个元素，返回 1。
2. 递归步骤：
   • 计算前 n-1 个元素的 LIS 长度 former。
   • 遍历前 n-1 个元素，如果某个元素 nums[i] 小于 nums[-1]，则递归计算 nums[:i+1] 的 LIS 长度，并尝试将 nums[-1] 添加到该子序列中。
   • 返回 former 和所有可能的 current_len 中的最大值。

示例验证

• nums = [10, 9, 2, 5, 3, 7, 101, 18]：
  • 递归会正确计算出最长子序列 [2, 3, 7, 101] 或 [2, 5, 7, 101]，返回 4。
• nums = [0, 1, 0, 3, 2, 3]：
  • 返回 4（如 [0, 1, 2, 3]）。
• nums = [7, 7, 7, 7]：
  • 返回 1（因为严格递增不允许重复）。

更优解法（动态规划）

递归解法效率太低，以下是动态规划的实现（推荐）：

from typing import List

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums:
            return 0
        
        dp = [1] * len(nums)
        for i in range(1, len(nums)):
            for j in range(i):
                if nums[j] < nums[i]:
                    dp[i] = max(dp[i], dp[j] + 1)
        
        return max(dp)

代码修复总结

1. 修复了缩进和语法错误。
2. 修正了递归逻辑，确保正确计算 LIS 长度。
3. 提供了动态规划的优化解法。