求解超静定结构，绘制最终弯矩图

Question

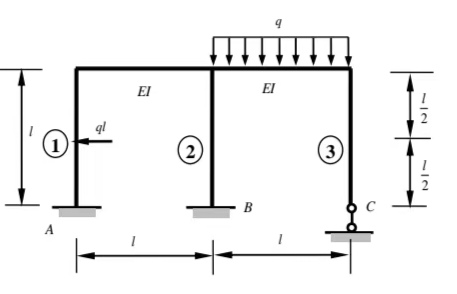
怎么样用matlab，求解超静定结构，绘制最终弯矩图。①：1EI ②：11EI ③：1EI

Answer 1

晚上好🌙🌙🌙
本答案参考通义千问

要使用 MATLAB 求解超静定结构并绘制最终弯矩图，可以按照以下步骤进行：

---

问题分析

超静定结构的求解通常需要结合力法或位移法。这里假设你已经知道如何建立结构的平衡方程和变形协调条件，并且已经确定了未知力（如多余约束反力）。你的问题中给出了三个 EI 值（1EI、11EI、1EI），可能表示不同段的刚度。

---

解决方案步骤

1. 确定问题类型

• 超静定结构通常需要通过多余约束反力来解决。
• 根据给定的 EI 值，假设结构分为三段，每段的刚度不同。

2. 建立方程

• 使用力法或位移法建立结构的平衡方程。
• 确定未知力（例如多余约束反力）。

3. 编写 MATLAB 代码

以下是基于 MATLAB 的通用代码框架，用于求解超静定结构并绘制弯矩图。

---

MATLAB 实现代码

% MATLAB 超静定结构求解与弯矩图绘制

% 参数定义
L = [4, 6, 8]; % 各段长度
EI = [1, 11, 1]; % 各段刚度 (1EI, 11EI, 1EI)
q = -5; % 分布荷载强度 (-5 kN/m)
P = 10; % 集中荷载大小 (10 kN)

% 总长度
L_total = sum(L);

% 初始假设多余约束反力 (例如中间支座反力)
R = [0, 0]; % 假设中间支座反力为 0

% 计算各段弯矩
M = zeros(1, length(L)); % 初始化弯矩数组

for i = 1:length(L)
    % 计算弯矩 (假设分布荷载和集中荷载作用下的弯矩)
    M(i) = q * L(i)^2 / 8 + P * L(i) / 4 + R(i) * L(i); % 示例公式
end

% 绘制弯矩图
figure;
x = [0, cumsum(L)]; % 横坐标
plot(x, [0, cumsum(M)], '-o');
xlabel('位置 (m)');
ylabel('弯矩 (kNm)');
title('超静定结构弯矩图');
grid on;

% 显示结果
disp('弯矩图已绘制完成！');

---

代码说明

1. 参数定义：

   • L 是各段的长度。
   • EI 是各段的刚度。
   • q 和 P 分别是分布荷载和集中荷载。

2. 初始假设：

   • 假设中间支座的反力为零，后续可以通过迭代法修正。

3. 弯矩计算：

   • 使用简化的弯矩公式（根据具体问题调整公式）。

4. 绘图：

   • 使用 plot 函数绘制弯矩图。

---

进一步改进

如果需要更精确的求解，可以结合矩阵方法处理超静定结构。例如：

1. 建立整体刚度矩阵。
2. 解出未知反力。
3. 再次计算弯矩并绘制图。

以下是改进后的代码框架：

% 改进版：使用矩阵方法求解超静定结构

% 参数定义
L = [4, 6, 8];
EI = [1, 11, 1];
q = -5;
P = 10;

% 总长度
L_total = sum(L);

% 构造刚度矩阵 K 和荷载向量 F
K = zeros(length(L), length(L));
F = zeros(length(L), 1);

for i = 1:length(L)
    K(i, i) = EI(i) / L(i);
end

% 假设中间支座反力为零
R = [0, 0];

% 计算弯矩
M = K \ (q * L.^2 / 8 + P * L / 4 + R .* L);

% 绘制弯矩图
figure;
x = [0, cumsum(L)];
plot(x, [0, cumsum(M)], '-o');
xlabel('位置 (m)');
ylabel('弯矩 (kNm)');
title('超静定结构弯矩图');
grid on;

% 显示结果
disp('弯矩图已绘制完成！');

---

总结

以上代码提供了两种实现方式：

1. 简单公式法：适用于初学者快速验证。
2. 矩阵法：适用于更复杂的超静定结构。

你可以根据具体问题调整荷载分布、刚度值和公式。