#数值模拟网格新画法

Question

#数值计算
一个半球网格（多层），外面套个立方体，不用极坐标得到，可以用什么方法得到，要保证它的球面的正交性，且顶部不会太密，想试着做数值模拟，希望可以Fortran语言，其他也可以

Answer 1

让【宝码香车】来帮你解答，本回答参考DeepSeek编写，并整理提供。

如果还有疑问可以点击头像关注私信或评论。如果答案让您满意，请采纳、点赞、关注，非常感谢！

数值模拟网格生成方法

对于半球网格(多层)外加立方体的数值模拟网格生成，同时保证球面正交性和避免顶部过于密集的问题，我可以推荐几种方法：

1. 贴体坐标法(Body-Fitted Coordinates)

这是最常用的方法之一，可以通过代数变换或微分方程方法生成贴体网格。

! Fortran 示例代码框架
program generate_grid
  implicit none
  integer, parameter :: n = 50  ! 网格点数
  real, dimension(n,n) :: x, y, z
  real :: r, theta, phi
  integer :: i, j
  
  ! 生成半球网格
  do i = 1, n
    do j = 1, n
      r = 1.0 + (i-1)*0.1  ! 径向多层
      theta = (j-1)*pi/(2*(n-1))  ! 纬度角
      phi = (i-1)*2*pi/(n-1)  ! 经度角
      
      ! 转换为直角坐标
      x(i,j) = r * sin(theta) * cos(phi)
      y(i,j) = r * sin(theta) * sin(phi)
      z(i,j) = r * cos(theta)
    end do
  end do
  
  ! 添加立方体外壳
  ! ...
end program generate_grid

2. 椭圆方程法(Elliptic Grid Generation)

通过求解椭圆型偏微分方程生成网格，可以保证正交性：

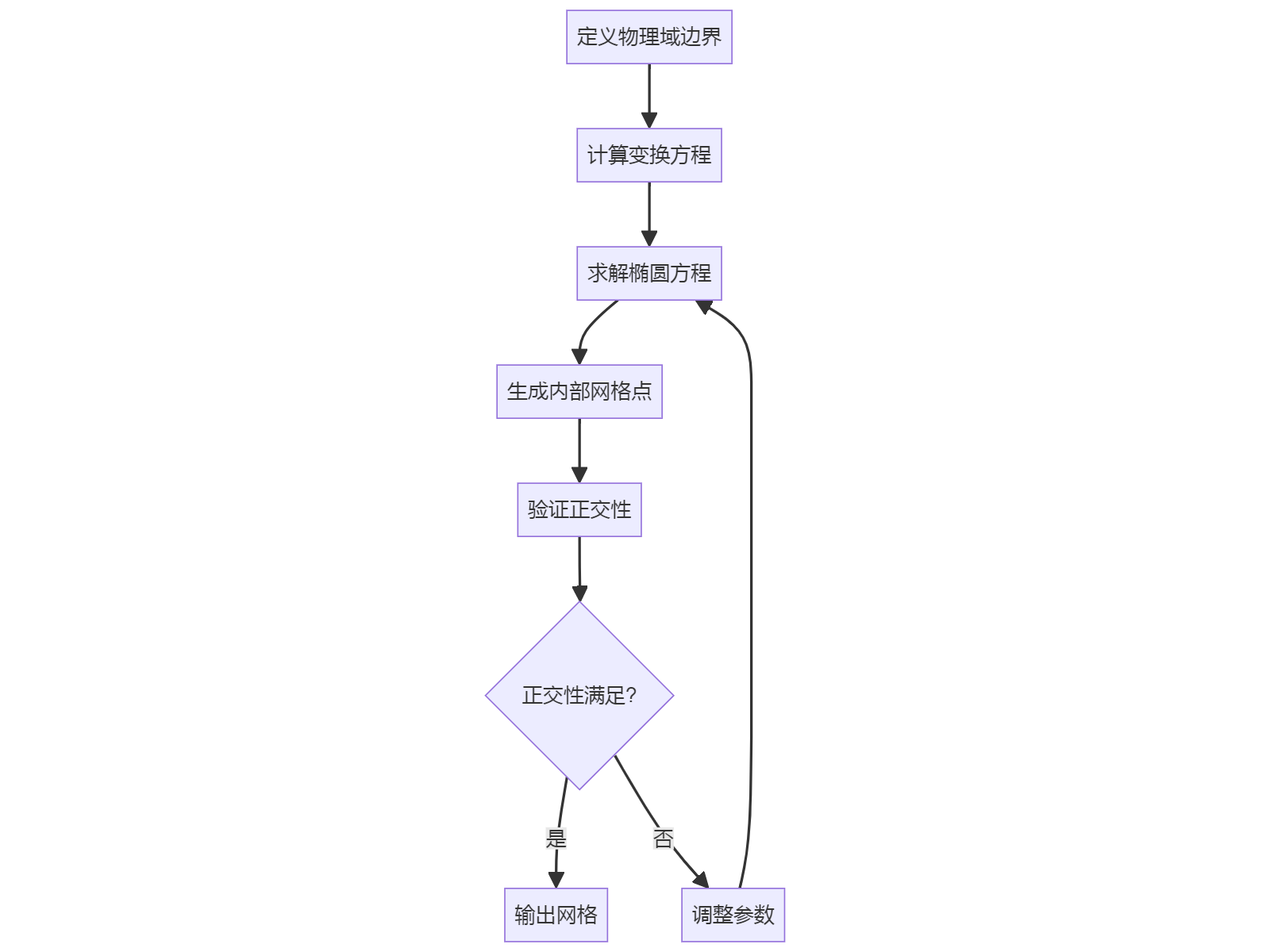
3. 复合网格法(Composite Grid)

将半球网格和立方体网格分开生成后组合：

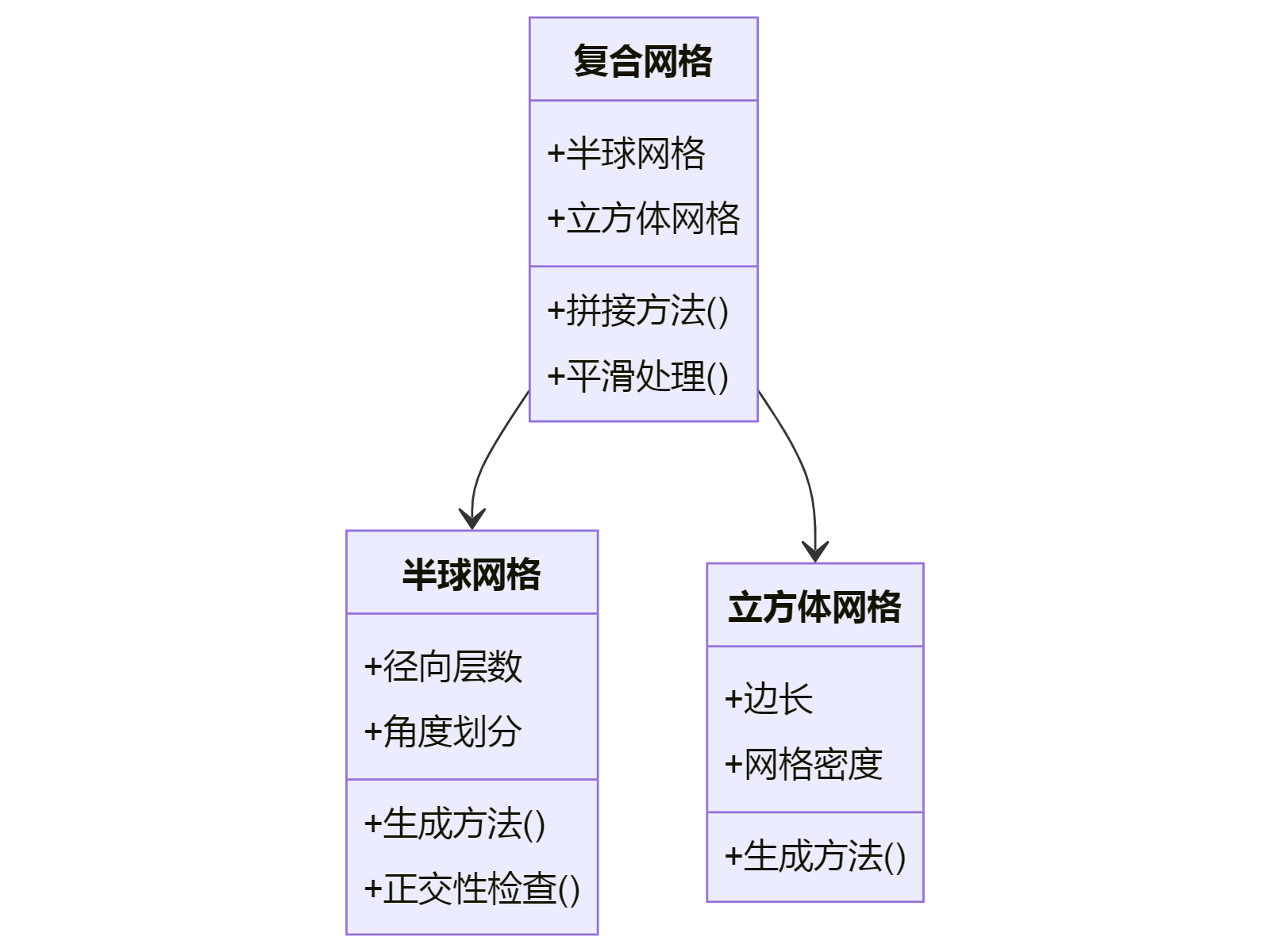
4. 其他语言实现参考

如果需要其他语言实现，Python也是一个好选择：

import numpy as np


def generate_hemisphere_grid(layers, points_per_layer):
    # 生成半球网格
    r = np.linspace(1.0, 2.0, layers)  # 径向坐标
    theta = np.linspace(0, np.pi/2, points_per_layer)  # 纬度角
    phi = np.linspace(0, 2*np.pi, points_per_layer)  # 经度角
    
    # 创建网格
    R, Theta, Phi = np.meshgrid(r, theta, phi, indexing='ij')
    
    # 转换为直角坐标
    x = R * np.sin(Theta) * np.cos(Phi)
    y = R * np.sin(Theta) * np.sin(Phi)
    z = R * np.cos(Theta)
    
    return x, y, z

关键注意事项

1. 正交性保证：
   • 使用椭圆方程法或贴体坐标法时，可以通过控制源项来调整正交性
   • 在边界处特别关注网格线的正交性

1. 顶部密度控制：
   • 使用非均匀角度划分，在顶部区域适当减少网格密度
   • 考虑使用对数或指数分布的角度划分

1. Fortran实现建议：
   • 使用模块化编程，将网格生成、正交性检查等功能分开
   • 考虑使用双精度计算提高精度
   • 对于大型网格，注意内存管理和并行计算

1. 验证方法：
   • 计算网格线的点积验证正交性
   • 可视化检查网格分布
   • 进行简单的数值测试验证网格质量

这些方法都可以避免直接使用极坐标，同时满足你的需求。具体选择哪种方法取决于你的具体应用场景和计算资源。