多边形区域盘管算法求解

Question

盘管总体需求包括多边形分割和区域盘管(包括生成过路管)。
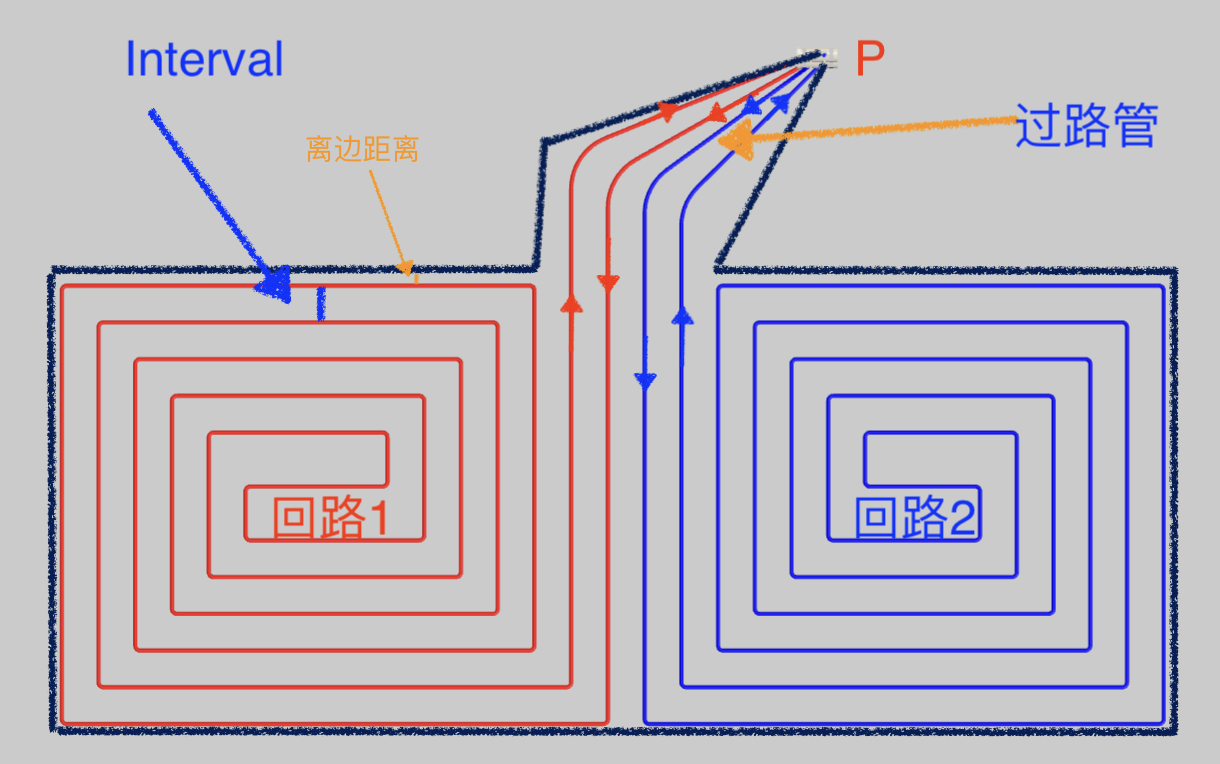
如图，给定一个多边形 （可以是凸或凹多边形，但不自相交），多边形内有一个点P（一般在边上）
a.从P点出发用多段线(也称管道)覆盖多边形的部分区域后回到P点,称为一个回路
b.从P出发和回到P的多个回路的相邻管道称为过路管

算法输入&输出
输入: 一组二维(x, y)点定义多边形和P点(x0, y0)，以及其它参数
输出: 一组对象。单个对象包括的数据有：子区域多边形边界点（x,y)的数组，多段线/管道的控制点（x,y)数组。
要求：
1.管道必须不交叉
2.尽量横平竖直或与边平行，美观度高
3.管道之间的距离尽量满足指定值(interval)
4.管道长度尽量相同，不超过指定值范围（minLength，maxLength）
5.过路管之间距离可以小于interval
6.管道不超过离边距离
7.拐弯尽量少

（本算法有预算，等你来承接）
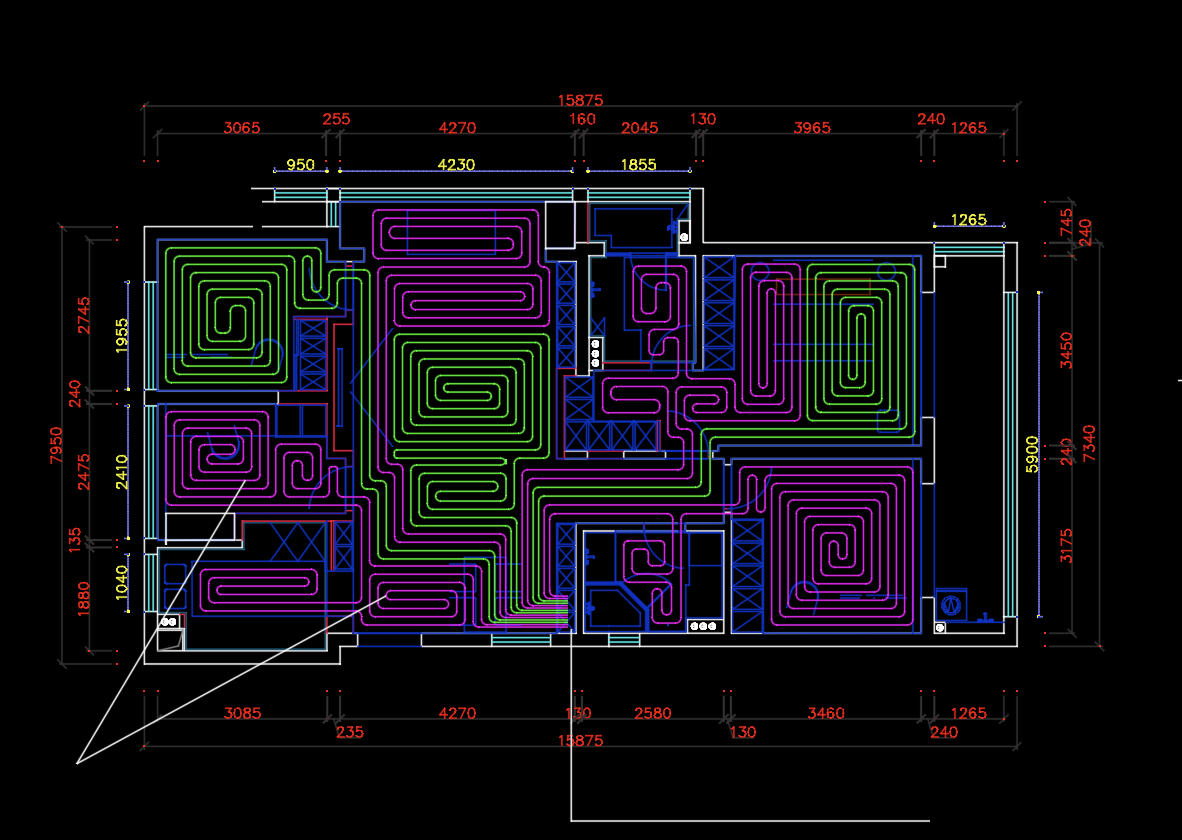
期望到达手动盘管的结果，如下图（多个房间连接成了一个多边形，如果需要房间信息，我们可提供，可以改算法参数）

Answer 1

阿里嘎多学长整理AIGC生成，因移动端显示问题导致当前答案未能完全显示，请使用PC端查看更加详细的解答过程

多边形区域盘管算法求解

你需要实现一个多边形区域盘管算法，用于将一个多边形分割成多个部分，并在每个部分内生成一条或多条管道，以覆盖该部分的区域。

这个问题可以分为两个部分：多边形分割和区域盘管。

1. 多边形分割：可以使用扫描线算法（Scan Line Algorithm）或分治算法（Divide and Conquer Algorithm）来分割多边形。
2. 区域盘管：可以使用栈算法（Stack Algorithm）或递归算法（Recursive Algorithm）来生成管道。

下面是一个使用栈算法实现的示例代码：

void regionPipe(int n, int* x, int* y) {
    // 初始化栈
    stack<int> s;
    s.push(0);

    // 遍历多边形的每个边
    for (int i = 0; i < n; i++) {
        // 如果栈不为空，且当前边与栈顶边相交
        while (!s.empty() && intersect(x[s.top()], y[s.top()], x[i], y[i])) {
            // 弹出栈顶边
            s.pop();
        }
        // 将当前边压入栈
        s.push(i);
    }

    // 生成管道
    while (!s.empty()) {
        int i = s.top();
        s.pop();
        // 生成管道
        // ...
    }
}

bool intersect(int x1, int y1, int x2, int y2) {
    // 判断两个点是否相交
    // ...
}

这个算法的基本思想是：从点P出发，使用栈算法将多边形分割成多个部分，每个部分对应一个管道。然后，使用递归算法生成每个部分的管道。

需要注意的是，这只是一个简单的示例代码，实际实现中可能需要根据具体情况进行修改和优化。