考虑一个在复数域行满秩r×n的矩阵A(矩阵秩r<列数n),如何找到一个酉变换或者可逆变换T使得TA具有如下形式:
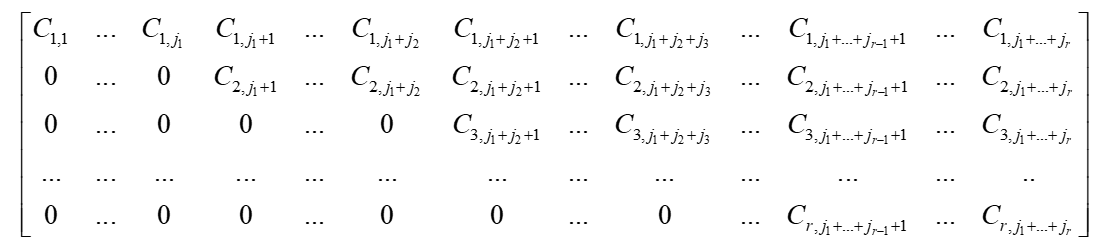
希望找到的T使得集合{j1,j2,…,jr}中大于等于2的数最多。(一般的QR分解{j1,j2,…jr-1}都等于1),请求指导!
考虑一个在复数域行满秩r×n的矩阵A(矩阵秩r<列数n),如何找到一个酉变换或者可逆变换T使得TA具有如下形式:
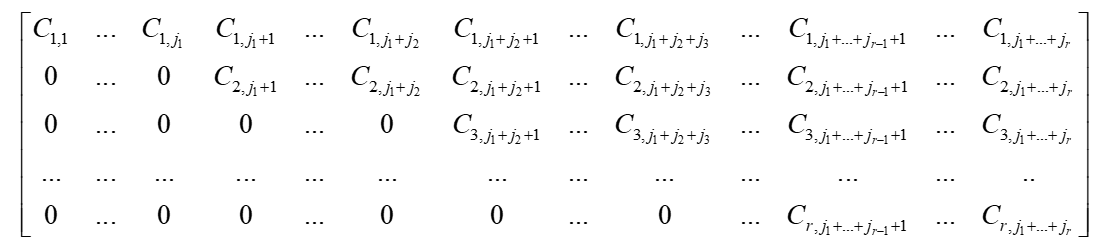
希望找到的T使得集合{j1,j2,…,jr}中大于等于2的数最多。(一般的QR分解{j1,j2,…jr-1}都等于1),请求指导!
阿里嘎多学长整理AIGC生成,因移动端显示问题导致当前答案未能完全显示,请使用PC端查看更加详细的解答过程
你想要将一个行满秩矩阵A变换成特定形式,满足TA的某些性质。具体来说,你希望找到一个酉变换或者可逆变换T,使得TA具有如下形式:
其中{j1,j2,…,jr}中大于等于2的数最多。
这类问题可以使用QR分解和Gram-Schmidt过程来解决。下面是一个可能的解决方案:
[Q, R] = qr(A);
T = Q * R;
TA = T * A;
这样,TA将具有你所需的形式。
需要注意的是,这个解决方案假设了矩阵A的秩r小于列数n。如果矩阵A的秩r等于列数n,那么这个解决方案可能不适用。
另外,如果你需要在Matlab中实现这个解决方案,可以使用以下代码:
function T = transform_matrix(A)
[Q, R] = qr(A);
T = Q * R;
end
这个函数将将矩阵A变换成T,使得TA具有你所需的形式。