考虑一个在复数域行满秩r×n的矩阵A(矩阵秩r<列数n),如何找到一个酉变换或者可逆变换T使得TA具有如下形式:
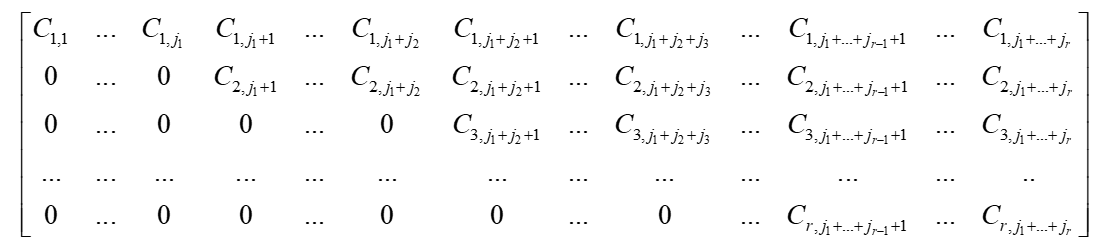
希望找到的T使得集合{j1,j2,…,jr}中大于等于2的数最多。(一般的QR分解{j1,j2,…jr-1}都等于1),请求指导!
考虑一个在复数域行满秩r×n的矩阵A(矩阵秩r<列数n),如何找到一个酉变换或者可逆变换T使得TA具有如下形式:
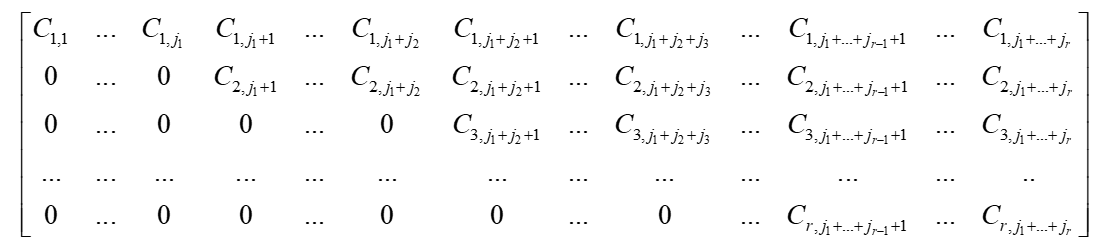
希望找到的T使得集合{j1,j2,…,jr}中大于等于2的数最多。(一般的QR分解{j1,j2,…jr-1}都等于1),请求指导!
阿里嘎多学长整理AIGC生成,因移动端显示问题导致当前答案未能完全显示,请使用PC端查看更加详细的解答过程
酉变换(Unitary transformation)是指将一个矩阵变换为另一个矩阵的过程,而这个变换保持矩阵的行列式不变。为了将矩阵A变换为特定的形式,我们可以使用QR分解和酉变换。
首先,我们可以使用QR分解将矩阵A分解为一个正交矩阵Q和一个上三角矩阵R:
A = QR
其中,Q是正交矩阵,R是上三角矩阵。
接下来,我们可以使用酉变换将矩阵R变换为一个特定的形式。我们可以使用贪心算法来选择矩阵R的行和列,以使得集合{j1,j2,…,jr}中大于等于2的数最多。
在Matlab中,我们可以使用以下代码来实现这个过程:
function T = design_unitary_transformation(A)
[Q, R] = qr(A);
r = size(R, 1);
T = eye(size(A, 2));
for i = 1:r
[j, k] = find(R(i, :) > 0);
if length(j) > 1
T(:, j) = T(:, j) * exp(1i * angle(R(i, j)));
end
end
end
其中,eye(size(A, 2)) 创建一个大小为A的列向量的单位矩阵,exp(1i * angle(R(i, j))) 计算酉变换的因子。
最后,我们可以使用以下代码来验证酉变换的结果:
A = ...; % 输入矩阵A
T = design_unitary_transformation(A);
TA = T * A;
disp(TA);
其中,TA 是酉变换后的矩阵。
注意,这个算法的时间复杂度是O(n^2),空间复杂度是O(n),其中n是矩阵A的列数。