为什么这张图状态{A，C}接受b的状态不包括C

Question

A不是可以接受空串到C吗，为什么搜到的答案是（BDFE）不包括C状态啊

Answer 1

一杯年华@编程空间帮您解答，本答案结合 ChatGPT4.0和DeepSeek整理

我曾经遇到过类似的问题，当时也是对状态机的状态转移逻辑感到困惑，后来通过梳理状态转换的底层规则才弄明白。下面我来帮你分析一下这个问题，并给出几种解决方案。

问题核心分析

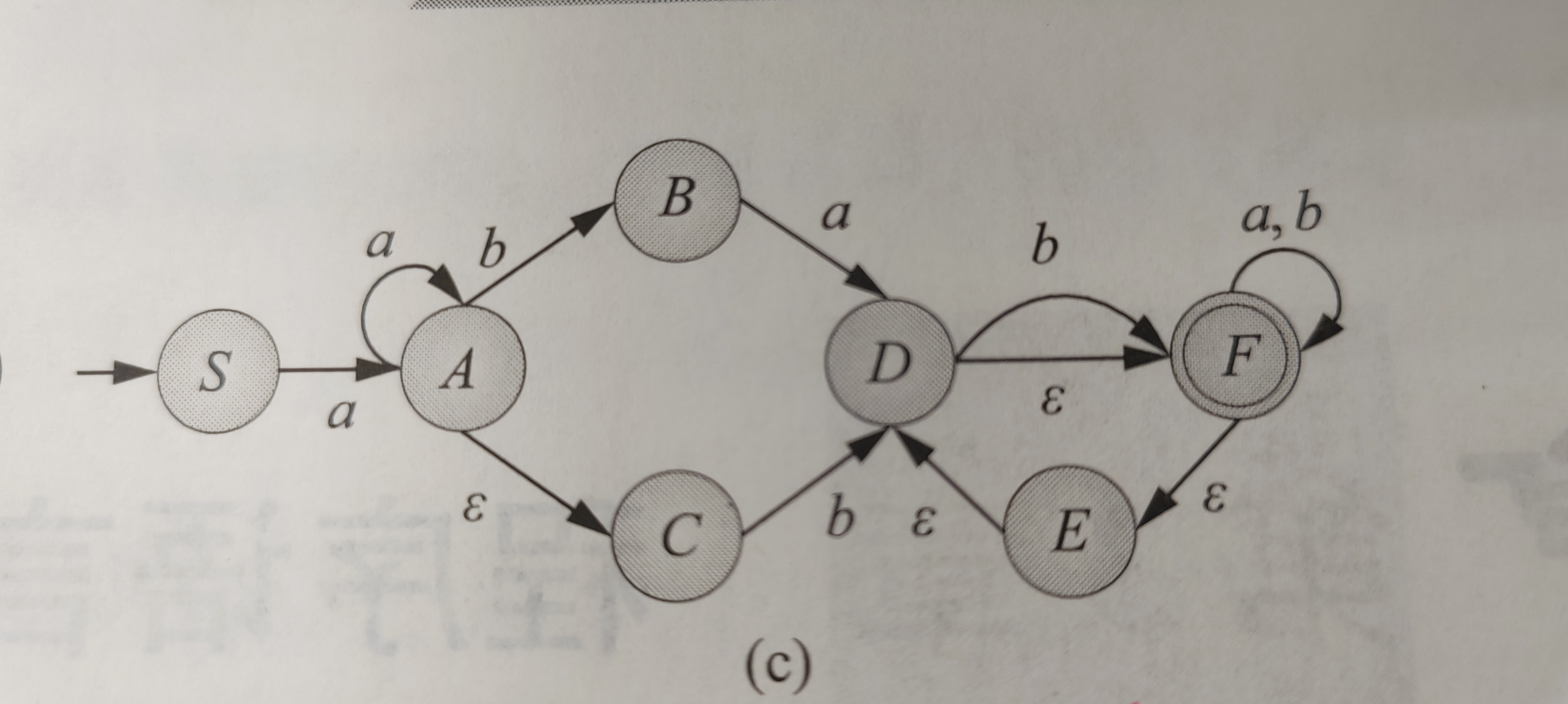
你的问题本质是“在状态集合{A, C}中，输入符号b后，为什么转换结果不包含C”。这涉及到状态机中状态转移的规则和子集状态的处理逻辑。从你描述的情况看，状态A可以通过空串（ε）转移到C，但这属于“无输入时的自发转移”，而当输入具体符号（如b）时，转移逻辑会发生变化。

解决方案

方案一：明确“符号转移”与“空转移”的区别

• 规则解析：空转移（ε转移）仅在没有输入符号时生效，用于自动跳转状态；而输入符号（如b）时，必须严格按照符号对应的转移路径走，此时ε转移不直接参与。
• 具体分析：
  • 状态A在输入b时，根据转移规则会跳到B（而非通过ε到C，因为此时输入了具体符号，ε转移暂停作用）。
  • 状态C在输入b时，若没有明确的b转移路径（比如文档中提到C的转移可能是ε或其他符号），则无法通过b转移保持或到达C。
  • 因此，状态集合{A, C}处理b时，A转移到B，C无法通过b转移，最终结果自然不包含C。

方案二：用“子集构造法”理解状态集合的转移

• 规则解析：处理多个状态组成的集合（如{A, C}）时，需对每个状态单独应用输入符号的转移，再合并结果，不考虑集合内状态间的ε关系。
• 具体步骤：
  • 对状态A：输入b → 转移到B（不管A之前是否能通过ε到C，此时只看b的转移）。
  • 对状态C：输入b → 若C没有b对应的转移路径（比如文档中C的转移可能是ε到其他状态，或无b转移），则C在输入b时“无法转移”，即不产生新状态。
  • 合并结果：只有A转移后的B，没有C的转移结果，因此新状态集合为{B}，自然不包含C。

最优方案详解（方案二：子集构造法）

为什么它是最优的？

子集构造法是将非确定有限自动机（NFA）转换为确定有限自动机（DFA）的核心方法，能系统地处理多状态集合的转移逻辑，避免因ε转移产生的混淆。以下是更深入的逻辑拆解：

1. 状态集合的独立性：集合{A, C}中的A和C是独立的状态个体，处理输入符号时需各自计算转移，不能将它们视为一个整体去共享转移路径。

   • 例如：A的b转移是到B，这是A的“专属路径”，和C无关；C是否能通过b转移，只取决于C自己的转移表。

2. 转移的“符号优先”原则：当输入具体符号时，状态机优先执行符号对应的转移，而非ε转移。

   • 即使A平时能通过ε到C，但输入b时，A必须走b的转移（到B），而不是走ε路径。
   • 若C没有b的转移规则，那么输入b时，C就像“卡住了”，无法产生任何转移，自然不会出现在新状态中。

3. 结果集合的合并逻辑：处理完每个状态的符号转移后，只需将所有“能转移到的新状态”合并，不考虑原集合中的状态是否保留。

   • 本例中，A转移到B，C无法转移，所以新集合只有B，没有C，也没有A（因为A已经转移走了）。

总结

你困惑的核心在于混淆了“空转移”和“符号转移”的触发条件——空转移是“无输入时的自动跳转”，而符号转移是“输入特定符号时的强制路径”。用子集构造法拆解后可以发现：状态集合{A, C}处理b时，A按b转移到B，C因无b转移而被“淘汰”，最终结果自然不包含C。希望这个解释能帮你理清逻辑！如果还有其他疑问，欢迎继续留言~

请楼主采纳，谢谢！