COMSOL 找不到初始参数的解，相对残差大于相对容差，已触发迭代求精，解不收敛为啥呀？

Question

COMSOL 找不到初始参数的解，相对残差大于相对容差，已触发迭代求精，返回的解不收敛，没有返回所有参数步长。
这是为什么呀？

Answer 1

让 “紫雾凌寒” 来帮你回答,本回答结合 DeepSeek

如果还有问题，请评论或点击头像私信，如果有帮助到您, 请关注、采纳、点赞

1. 关键点分析：
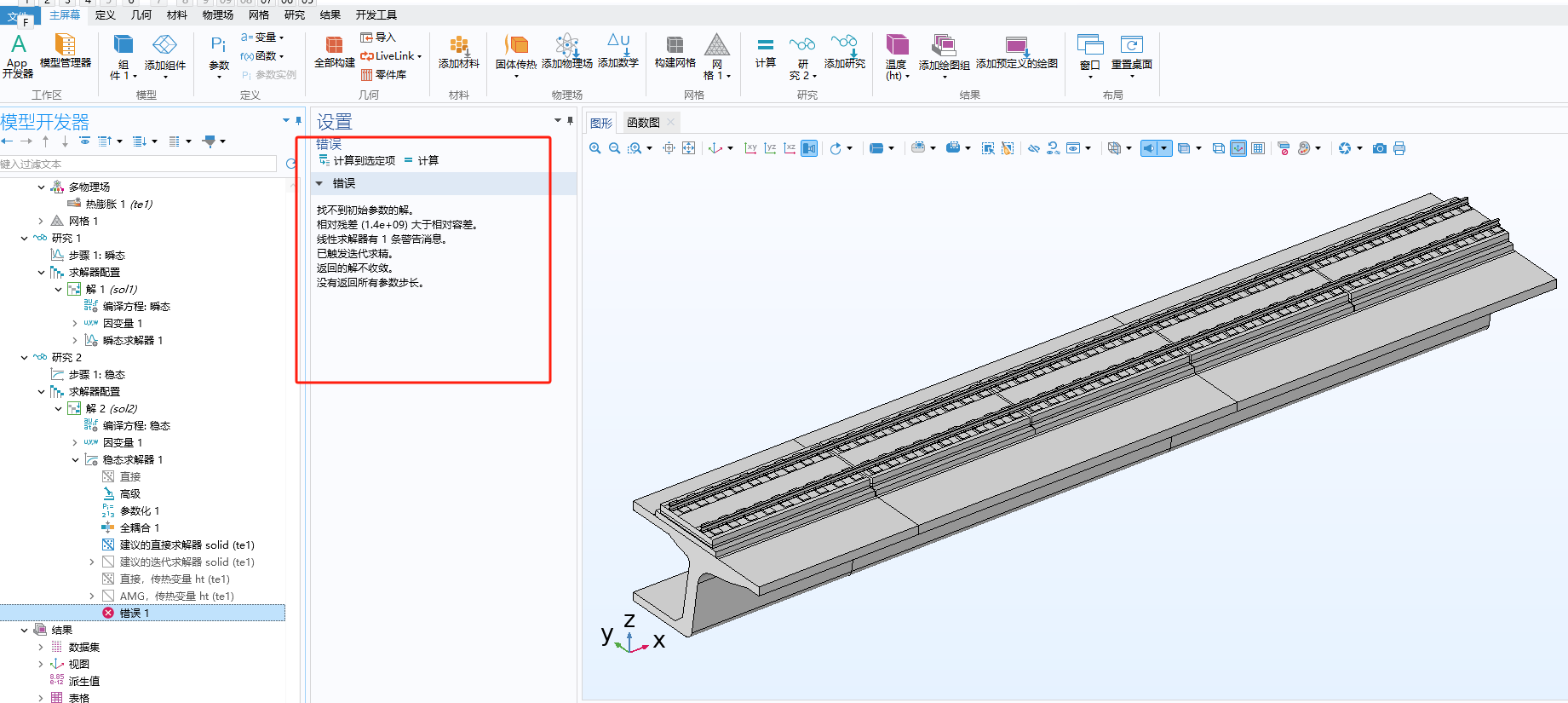
   - 核心问题在于COMSOL求解时找不到初始参数的解，相对残差超出相对容差且解不收敛，同时未返回所有参数步长。这可能涉及到模型设置、物理场定义、边界条件、初始猜测值以及求解器设置等多方面的因素。
2. 解决方案：
   - 检查模型设置：
   • 确认物理场定义是否正确。例如，如果是多物理场耦合问题，要确保各个物理场之间的相互作用设置无误。比如在热 - 结构耦合中，热传递系数等参数是否合理。
   • 检查边界条件是否准确反映实际情况。不合适的边界条件可能导致求解困难。例如，在模拟传热问题时，边界的温度设定是否符合实际工况。
   • 初始猜测值调整：
   • 为参数提供更合理的初始猜测值。如果初始值偏离真实解太远，求解器可能难以收敛。比如对于一个涉及材料属性的参数，如果初始猜测值与实际材料属性相差很大，就可能出现收敛问题。
   • 可以通过对相关物理量的初步分析或经验来确定初始猜测值。例如，对于一个电场分布问题，可以根据类似结构的已有结果来估计电场强度的初始值。
   • 求解器设置优化：
   • 调整求解器的参数，如相对容差和绝对容差。适当减小容差可能有助于收敛，但过小的容差会增加计算时间。例如，将相对容差从默认的(1e - 3)减小到(1e - 4)进行尝试。
   • 选择合适的求解器类型。不同的求解器适用于不同类型的问题。如果是线性问题，直接求解器可能更高效；对于非线性问题，迭代求解器可能更合适。例如，对于一个线性方程组，可以尝试使用共轭梯度法（CG）求解器，对于非线性问题，可以使用牛顿法等迭代求解器，并根据具体情况调整其参数。
   • 检查模型的连续性和光滑性：
   • 确保模型在几何形状、材料属性等方面具有连续性和光滑性。不连续或奇异的模型可能导致求解失败。例如，避免材料属性在模型中突然变化而没有合理的过渡。
   • 检查模型中是否存在微小的几何缺陷或不合理的尺寸设置，这些可能影响求解结果。比如，非常小的孔洞或间隙可能导致数值计算不稳定。
3. 不同解决方案的优缺点：
   - 检查模型设置：
   • 优点：从根本上解决问题，如果模型设置错误，修正后可以使求解过程顺利进行，结果更可靠。
   • 缺点：需要对模型的物理原理和边界条件有深入理解，排查过程可能较繁琐，尤其是复杂模型。
   • 初始猜测值调整：
   • 优点：相对容易操作，通过合理调整初始值可能快速改善收敛情况。
   • 缺点：对于复杂问题，很难准确估计初始值，可能需要多次尝试和经验积累。
   • 求解器设置优化：
   • 优点：可以直接针对求解过程进行调整，有可能在不改变模型本身的情况下解决收敛问题。
   • 缺点：需要对求解器有一定了解，调整不当可能导致计算效率降低甚至无法求解。
   • 检查模型的连续性和光滑性：
   • 优点：有助于发现模型中的潜在问题，保证模型的合理性，从而使求解更稳定。
   • 缺点：需要仔细检查模型的各个方面，对于大型复杂模型工作量较大。
4. 总结：
   - COMSOL求解不收敛且找不到初始参数解的问题可能由多种原因引起。通过检查模型设置、调整初始猜测值、优化求解器设置以及确保模型的连续性和光滑性等方面进行排查和解决。在实际操作中，可能需要综合运用这些方法，逐步找到问题所在并解决，以获得可靠的求解结果。

例如，在一个简单的传热模型中，如果发现解不收敛：

model = Model('HeatTransferModule');
geom = model.Geometry;
% 定义几何形状
geom.Box(0, 0, 0, 1, 1, 1);
% 定义材料属性
mat = model.Materials('Material1');
mat.ThermalConductivity = 1;
% 定义边界条件
bc1 = model.BoundaryConditions('BoundaryCondition1');
bc1.Temperature = 0;
bc2 = model.BoundaryConditions('BoundaryCondition2');
bc2.Temperature = 100;
% 初始猜测温度场
T0 = zeros(100, 100, 100);
% 设置求解器
solver = model.Solvers('Stationary');
solver.RelativeTolerance = 1e - 4;

在上述代码中，首先检查了模型的几何形状、材料属性和边界条件定义是否正确。然后设置了初始猜测温度场，并调整了求解器的相对容差，通过这些操作来尝试改善求解的收敛情况。

希望以上解答对您有所帮助。如果您有任何疑问，欢迎在评论区提出。