数学建模窗框切割最优切割方案

Question

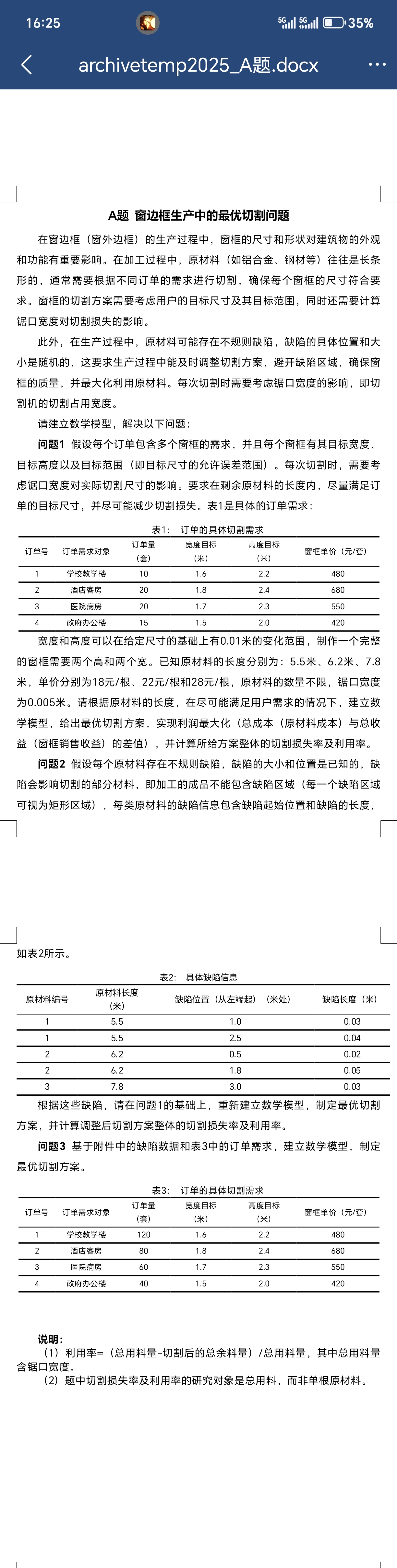
这道数学建模题怎么确定代码跑出来的结果在正确答案范围内 还有没有什么建模思路 目前用的是线性规划

Answer 1

让 “紫雾凌寒” 来帮你回答,本回答结合 DeepSeek

如果还有问题，请评论或点击头像私信，如果有帮助到您, 请关注、采纳、点赞

1. 关键点分析：
   - 要确定代码跑出来的结果是否在正确答案范围内，需要有一个明确的“正确答案范围”的界定方法。这可能涉及到对问题的理论最优解的推导，或者已知的一些可行解边界条件。
   - 建模思路方面，除了线性规划，还可以考虑其他方法。比如动态规划，它适用于解决具有重叠子问题和最优子结构性质的问题；整数规划，当决策变量需要取整数值时可能更合适；甚至可以尝试启发式算法，如遗传算法、模拟退火算法等，这些算法能在复杂问题中快速找到较优解。
2. 解决方案：
   - 确定结果范围的方法：
   • 理论最优解推导：
   • 对于窗框切割问题，首先分析切割的目标。例如，如果是要使材料利用率最高，设窗框的不同规格尺寸为(a_1,a_2,\cdots,a_n)，材料长度为(L)。
   • 假设每种窗框需要的数量为(x_1,x_2,\cdots,x_n)，则约束条件可以是(\sum_{i = 1}^{n}a_ix_i\leq L)。
   • 通过理论分析，当不产生废料时，能得到一个理论上的最大利用率情况。比如，如果所有窗框规格都是整数，且材料长度(L)能被窗框某一规格整除，那么按照该规格进行切割就是理论最优解。
   • 已知可行解边界条件：
   • 可以通过一些简单的计算得到可行解的边界。例如，先假设只切割一种窗框规格，计算出最多能切割的数量，这就是一个边界值。然后逐步增加窗框规格种类，通过试错法或者简单的数学计算确定不同规格组合下的可行解范围。
   • 不同建模方法示例：
   • 线性规划：
   • 设(x_{ij})表示第(i)种切割方式下第(j)种窗框的切割数量。
   • 目标函数：假设是要最大化窗框的总数量(Z=\sum_{j = 1}^{m}\sum_{i = 1}^{k}x_{ij})（这里(m)是窗框种类，(k)是切割方式种类）。
   • 约束条件：
     • 材料长度约束：(\sum_{j = 1}^{m}a_jx_{ij}\leq L_i)，其中(a_j)是第(j)种窗框的长度，(L_i)是第(i)种切割方式下材料的长度。
     • 非负约束：(x_{ij}\geq0)，(i = 1,\cdots,k)，(j = 1,\cdots,m)。
   • 可以使用Python的PuLP库来求解线性规划问题，代码示例如下：

import pulp

# 创建问题实例
problem = pulp.LpProblem("窗框切割问题", pulp.LpMaximize)

# 定义决策变量
x = pulp.LpVariable.dicts("x", [(i, j) for i in range(k) for j in range(m)], lowBound = 0)

# 定义目标函数
problem += pulp.lpSum([x[(i, j)] for j in range(m) for i in range(k)])

# 定义约束条件
for i in range(k):
    problem += pulp.lpSum([a[j]*x[(i, j)] for j in range(m)]) <= L[i]

# 求解问题
problem.solve()

# 输出结果
for i in range(k):
    for j in range(m):
        print(f"第{i}种切割方式下第{j}种窗框的数量: {pulp.value(x[(i, j)])}")
print(f"目标函数最大值: {pulp.value(problem.objective)}")

 - **动态规划**：
   - 设\(dp[i]\)表示长度为\(i\)的材料能得到的最大窗框数量。
   - 状态转移方程：\(dp[i]=\max_{j = 1}^{m}(dp[i - a_j]+1)\)，其中\(a_j\)是第\(j\)种窗框的长度。
   - 边界条件：\(dp[0]=0\)。
   - 代码示例：

dp = [0] * (L + 1)
for i in range(1, L + 1):
    for a in a_list:
        if i >= a:
            dp[i] = max(dp[i], dp[i - a]+1)
print(dp[L])

 - **整数规划**：
   - 目标函数和约束条件与线性规划类似，但决策变量\(x_{ij}\)要求为整数。
   - 可以使用Python的`scipy.optimize`库中的`linprog`函数来求解整数规划问题（这里需要使用混合整数规划求解器，如`glpk`等），示例代码如下：

from scipy.optimize import linprog

# 定义目标函数系数
c = [-1] * (k * m)

# 定义不等式约束系数矩阵A和向量b
A = []
b = []
for i in range(k):
    row = [a[j] if j < m else 0 for j in range(k * m)]
    A.append(row)
    b.append(L[i])

# 定义等式约束系数矩阵Aeq和向量beq（这里假设没有等式约束）
Aeq = []
beq = []

# 定义决策变量的上下界
x0_bounds = [(0, None)] * (k * m)

# 求解整数规划
res = linprog(c, A_ub = A, b_ub = b, A_eq = Aeq, b_eq = beq, bounds = x0_bounds, integrality = list(range(k * m)))

# 输出结果
x_sol = res.x.reshape(k, m)
print(x_sol)
print(-res.fun)

1. 不同方案优缺点：
   - 线性规划：
   • 优点：理论成熟，求解算法高效，能得到全局最优解（如果有解），适用于大规模问题。
   • 缺点：对问题的线性假设要求严格，如果实际问题是非线性的，可能需要进行复杂的线性化处理。
   • 动态规划：
   • 优点：能有效解决具有最优子结构性质的问题，避免了一些冗余计算，对于规模不是特别大的问题求解速度较快。
   • 缺点：状态转移方程的推导可能比较复杂，需要对问题有深入的理解，而且空间复杂度可能较高，对于大规模问题可能内存消耗较大。
   • 整数规划：
   • 优点：适合决策变量为整数的情况，能直接得到符合实际意义的整数解。
   • 缺点：求解难度较大，计算时间较长，尤其是对于大规模问题，可能会遇到计算瓶颈。
   • 启发式算法：
   • 优点：能在较短时间内找到较优解，对问题的模型要求相对较低，适用于复杂的非线性问题。
   • 缺点：不能保证得到全局最优解，解的质量依赖于算法参数的设置和初始条件。
2. 总结：
   - 要确定代码结果是否在正确答案范围内，需要通过理论最优解推导或确定可行解边界条件。
   - 建模思路除了线性规划外，动态规划、整数规划和启发式算法等也可用于窗框切割最优切割方案问题，各有优缺点，应根据问题特点选择合适的方法。

通过以上方法，可以更好地解决数学建模窗框切割最优切割方案问题，并对得到的结果进行有效的验证和评估。

希望以上解答对您有所帮助。如果您有任何疑问，欢迎在评论区提出。