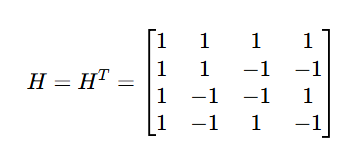h.264中,二维 4×4 Hadamard 变换的算法实现公式是什么呢?即Y各个位置上的坐标值,Y00,Y01,...,Y33完整的公式是什么呢?
Y=HXHT.
假设:
X = [x00, x01, x02, x03]
[x10, x11, x12, x13]
[x20, x21, x22, x23]
[x30, x31, x32, x33]
H=HT=[1, 1, 1, 1]
[1, 1, -1, -1]
[1, -1, -1, 1]
[1, -1, 1, -1]