让 “紫雾凌寒” 来帮你回答,本回答结合 DeepSeek
如果还有问题,请评论或点击头像私信,如果有帮助到您, 请关注、采纳、点赞
- 关键点分析:
- 问题聚焦于H.264标准中逆离散余弦变换(IDCT)输出各位置的具体公式。需要准确理解IDCT的原理和相关系数,按照给定的矩阵索引形式(如Xr00 - Xr33)来推导具体公式。 - 解决方案:
- H.264中的4x4 IDCT变换公式如下:- (X_{r00}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i0}C_{j0}x_{ij})
- (X_{r01}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i0}C_{j1}x_{ij})
- (X_{r02}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i0}C_{j2}x_{ij})
- (X_{r03}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i0}C_{j3}x_{ij})
- (X_{r10}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i1}C_{j0}x_{ij})
- (X_{r11}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i1}C_{j1}x_{ij})
- (X_{r12}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i1}C_{j2}x_{ij})
- (X_{r13}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i1}C_{j3}x_{ij})
- (X_{r20}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i2}C_{j0}x_{ij})
- (X_{r21}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i2}C_{j1}x_{ij})
- (X_{r22}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i2}C_{j2}x_{ij})
- (X_{r23}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i2}C_{j3}x_{ij})
- (X_{r30}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i3}C_{j0}x_{ij})
- (X_{r31}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i3}C_{j1}x_{ij})
- (X_{r32}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i3}C_{j2}x_{ij})
- (X_{r33}=\frac{1}{4}\sum_{i = 0}^{3}\sum_{j = 0}^{3}a_{ij}C_{i3}C_{j3}x_{ij})
- 其中,(C_{i0}=\sqrt{\frac{1}{2}}),(C_{i1}=\sqrt{\frac{1}{2}}),(C_{i2}=\sqrt{\frac{1}{2}}),(C_{i3}=\sqrt{\frac{1}{2}}),(a_{ij})是根据不同的变换阶段有不同取值的系数矩阵(具体系数值可参考H.264标准文档),(x_{ij})是输入的4x4块的系数。
- 多种解决方案及优缺点:
- 直接使用标准公式:- 优点:最准确地符合H.264标准,能够直接实现IDCT变换,适用于严格按照标准进行编解码开发的场景。
- 缺点:公式较为复杂,计算量较大,实现过程中可能需要仔细处理系数和索引,容易出现计算错误。
- 使用优化算法:
- 优点:可以减少计算量,提高计算效率,例如一些快速IDCT算法。
- 缺点:可能需要对算法进行深入理解和优化才能正确实现,并且可能与标准公式存在一定的误差,需要根据具体应用场景权衡精度和效率。
- 总结:
- H.264的IDCT变换输出各位置的公式是基于离散余弦变换原理,并结合特定系数矩阵的复杂求和公式。在实际实现中,可根据具体需求选择直接使用标准公式或优化算法来完成IDCT变换,以平衡计算精度和效率。
需要注意的是,实际实现时还需考虑数据类型、边界处理等细节问题,以确保编解码的正确性和稳定性。
希望以上解答对您有所帮助。如果您有任何疑问,欢迎在评论区提出。
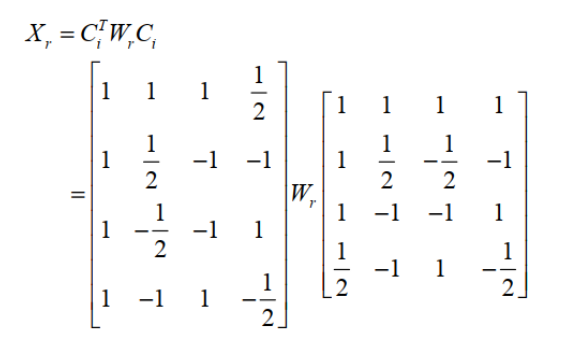
 关注
关注