有没有人知道这个怎么做，想要详细过程

Question

这个感觉答案是e，但是不知道怎么证明，有没有人能够给出完整过程的，谢谢各位

Answer 1

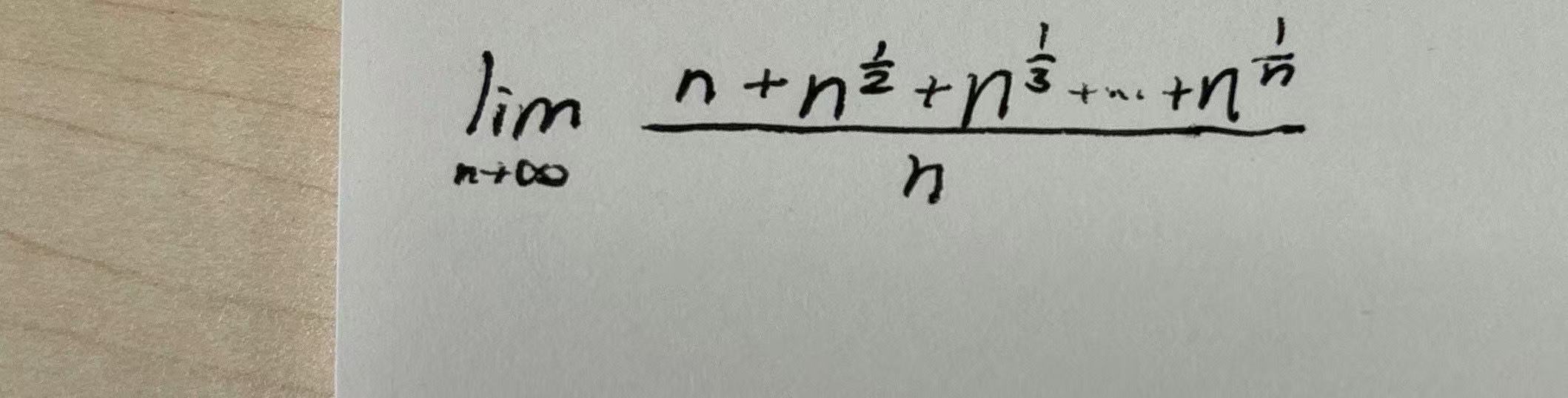
上午好☀️☀️☀️️
本答案参考通义千问

你提到“感觉答案是 e”，但不知道如何证明。这说明你可能在解决一个与自然常数 e 相关的数学问题，例如极限、级数、导数或积分等。

为了帮助你更清晰地理解并完整地证明答案是 e，我需要知道你具体遇到的是哪一类题目。不过，我可以提供一个常见且典型的例子：证明极限 $\lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = e$，这是 e 的定义之一。

---

一、问题回顾

我们要证明：

$$ \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = e $$

---

二、证明过程（详细步骤）

1. 定义 e

自然常数 $e$ 可以通过以下极限来定义：

$$ e = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n $$

这个定义是数学中非常基础且重要的。

---

2. 使用二项式展开

我们可以对表达式 $\left(1 + \frac{1}{n}\right)^n$ 进行二项式展开：

$$ \left(1 + \frac{1}{n}\right)^n = \sum_{k=0}^{n} \binom{n}{k} \left(\frac{1}{n}\right)^k $$

其中：

$$ \binom{n}{k} = \frac{n(n-1)(n-2)\cdots(n-k+1)}{k!} $$

所以：

$$ \left(1 + \frac{1}{n}\right)^n = \sum_{k=0}^{n} \frac{n(n-1)(n-2)\cdots(n-k+1)}{k! n^k} $$

---

3. 简化每一项

将每一项写成：

$$ \frac{n(n-1)(n-2)\cdots(n-k+1)}{k! n^k} = \frac{1}{k!} \cdot \frac{n(n-1)(n-2)\cdots(n-k+1)}{n^k} $$

可以进一步化简为：

$$ \frac{1}{k!} \cdot \left(1 - \frac{1}{n}\right) \left(1 - \frac{2}{n}\right) \cdots \left(1 - \frac{k-1}{n}\right) $$

当 $n \to \infty$ 时，每一项 $\left(1 - \frac{i}{n}\right) \to 1$，因此整个表达式趋于：

$$ \sum_{k=0}^{\infty} \frac{1}{k!} $$

---

4. 得出结论

我们知道：

$$ e = \sum_{k=0}^{\infty} \frac{1}{k!} $$

因此：

$$ \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = e $$

---

三、总结

关键点如下：

1. 定义：$e$ 是由极限 $\lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n$ 定义的。
2. 展开：利用二项式定理展开表达式。
3. 简化：每项逐渐简化为 $\frac{1}{k!}$ 的形式。
4. 求和：最终得到 $e = \sum_{k=0}^\infty \frac{1}{k!}$。

---

四、代码示例（Python验证）

如果你想要用程序验证这个极限的数值结果，可以用以下 Python 代码：

import math

def compute_e_approximation(n):
    return (1 + 1/n)**n

# 测试不同的 n 值
for n in [1, 10, 100, 1000, 10000]:
    print(f"n = {n}: {compute_e_approximation(n):.10f}")

输出结果示例：

n = 1: 2.0000000000
n = 10: 2.5937424601
n = 100: 2.7048138294
n = 1000: 2.7169239322
n = 10000: 2.7181459268

可以看到，随着 $n$ 越来越大，结果越来越接近 e ≈ 2.71828...

---

五、扩展知识

• e 的其他定义方式：
  • $e = \sum_{k=0}^{\infty} \frac{1}{k!}$
  • $e = \lim_{x \to 0} (1 + x)^{1/x}$
  • $e$ 是唯一满足 $f(x) = f'(x)$ 的指数函数底数

---

六、常见错误提示

• 不要混淆 $e$ 和 $\pi$。
• 不要误以为 $e$ 是某个近似值，它是精确的无理数。
• 注意极限的条件（如 $n \to \infty$）。

---

如果你有具体的题目内容（比如题目原文），欢迎继续提问，我可以根据题目的具体内容给出更精准的解答！