西交870集成电路考研，我看到这个问题有两种回答，到底是哪个啊

Question

考研儿，我看到这个问题有两种回答，一种是√(3H/4)，一种是√(4H/3)，因为是跟着PPT学的，没看书，所以我只看懂了前者的解答过程，后者不太懂，而且后者我算出来答案也是√(3H/4)，到底是哪个啊

Answer 1

让【宝码香车】来帮您解答，本回答参考DeepSeek编写，并整理提供。

如果答案让您满意，请采纳、点赞、关注，非常感谢！
.
每日一句正能量，让它带给您好心情：生活的美好，在于它的不确定性，你永远不知道下一秒会有什么惊喜。
.

根据你提供的题目信息和两种解法，我来帮你分析一下正确答案应该是哪个。

问题分析

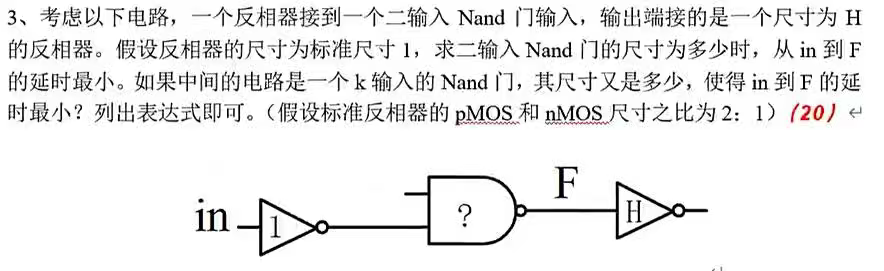
题目描述的是一个反相器接到一个二输入NAND门输入，输出端接一个尺寸为H的反相器。要求找到使从输入到输出的延时最小的NAND门尺寸。

关键参数

• 标准反相器的pMOS和nMOS尺寸之比为2:1
• 二输入NAND门的逻辑努力需要计算

逻辑努力计算

对于二输入NAND门：

• nMOS网络：2个nMOS串联，每个尺寸为1，总导通电阻相当于2个单位
• pMOS网络：2个pMOS并联，每个尺寸为2（因为pMOS:nMOS=2:1），总导通电阻相当于1个单位

因此，二输入NAND门的逻辑努力：

• 输入A/B对输出上升沿：2/3 ≈ 0.67
• 输入A/B对输出下降沿：4/3 ≈ 1.33
• 通常取较大值，所以逻辑努力g = 4/3

正确解法

路径努力F = 逻辑努力G × 电气努力H × 分支努力B

这里：

• G = g₁ × g₂ = (1) × (4/3) = 4/3（第一级反相器逻辑努力为1，第二级NAND门为4/3）
• H = C_out/C_in = H/1 = H
• B = 1（无分支）

所以F = (4/3) × H × 1 = 4H/3

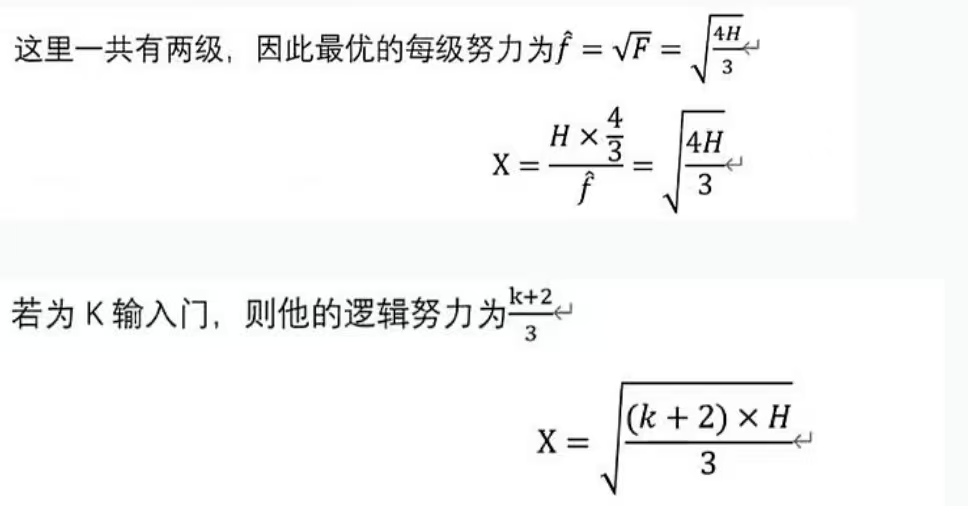
对于两级电路，最优每级努力f = √F = √(4H/3)

第一级反相器到NAND门的努力应为f，即：

电气努力h₁ = f/g₁ = √(4H/3) / 1 = √(4H/3)

NAND门尺寸 = 输入电容 = 驱动该门的反相器尺寸 / h₁
由于驱动NAND门的是标准反相器（尺寸1），所以：

NAND门尺寸 = 1 / √(4H/3) = √(3/4H)

结论

**正确答案是√(3H/4)**。

你提到的√(4H/3)可能是对最优每级努力的误解，而√(3H/4)才是NAND门的正确尺寸表达式。

对于k输入NAND门的情况，逻辑努力g = (k+2)/3，你可以用同样的方法推导出通用表达式。