束腰为σ的高斯光束表达式如何影响远场发散角？

Question

在高斯光束传播特性分析中，束腰半径σ直接影响其远场发散角。已知高斯光束的远场发散角θ ≈ λ / (πσ)，其中λ为波长。当束腰σ减小时，为何远场发散角显著增大？这种关系在激光准直、光纤耦合等应用中尤为关键。请结合高斯光束的传播公式，解释束腰尺寸与发散角之间的物理机制，并说明为何极小的束腰会导致光束快速发散，这对光学系统设计带来哪些挑战？

Answer 1

让【宝码香车】来帮你解答，本回答参考DeepSeek编写，并整理提供。

如果还有疑问可以“评论”。如果答案让您满意，请“采纳”，非常感谢！

在高斯光束传播特性中，束腰半径σ与远场发散角θ之间的关系由公式θ ≈ λ / (πσ)描述，其中λ为波长。当σ减小时，θ显著增大，这是由于衍射效应导致的物理现象。以下结合高斯光束传播公式解释这一机制，并讨论在光学系统设计中的挑战。

1. 束腰与发散角的关系公式

高斯光束的远场发散角θ定义为光束半径在远场（传播距离z远大于瑞利范围z_R）的渐近线斜率。从高斯光束传播方程出发：

• 光束半径w(z)随传播距离z变化：w(z) = σ √(1 + (z / z_R)²)，其中σ为束腰半径（即w₀），z_R = π σ² / λ为瑞利范围。
• 在远场（z >> z_R），w(z) ≈ (λ / (πσ)) z，因此发散角θ = lim_{z→∞} w(z)/z = λ / (πσ)。

从公式可见，θ与σ成反比：σ减小则θ增大。例如，当波长λ固定时，σ减半会导致θ加倍。

2. 物理机制：衍射效应

高斯光束是衍射受限的光束，其发散行为由衍射原理支配：

• 束腰尺寸与衍射：束腰处光束被限制在极小区域，根据傅里叶光学，空间限制越强（σ越小），空间频率谱越宽，导致远场衍射角越大。这类似于小孔衍射：孔径越小，衍射斑越大。
• 瑞利范围的作用：瑞利范围z_R = π σ² / λ表示光束保持准直的距离。σ减小时，z_R急剧减小（z_R ∝ σ²），意味着光束更快地进入发散阶段，从而远场发散角更大。
• 波前曲率：在束腰处，波前为平面；随着传播，波前曲率增大，光束发散。小σ导致波前曲率变化更剧烈，加速发散。

物理上，极小的束腰（如微米级）会使光束在短距离内迅速扩展，这对需要长距离传输的应用不利。

3. 光学系统设计中的挑战

在激光准直、光纤耦合等应用中，束腰与发散角的关系带来以下挑战：

• 激光准直：为了获得小发散角（如用于激光雷达或通信），需要大束腰（σ大），但大束腰要求光学元件（如透镜）尺寸大，增加系统体积和成本。同时，大束腰可能降低能量密度，影响效率。
• 光纤耦合：单模光纤的模场直径小（通常约10μm），需要小束腰以匹配模式，但小σ导致大发散角，使得耦合效率对对准误差非常敏感（如微米级偏移可能导致显著损耗）。设计时需权衡束腰尺寸和容忍度。
• 光束质量与系统稳定性：极小束腰易受环境扰动（如热漂移、振动）影响，导致光束指向不稳定。此外，在非线性光学中，小束腰可能引发非线性效应（如自聚焦），损坏元件。
• 设计优化：工程师需通过透镜系统调整束腰位置和尺寸，但σ和θ的权衡常需复杂模拟。例如，使用扩束镜增大σ以减少θ，但会引入额外光学面，增加像差和损耗。

4. 代码示例：计算发散角

以下Python代码演示束腰半径σ对远场发散角θ的影响，假设波长λ=632.8 nm（He-Ne激光）：

import numpy as np
import matplotlib.pyplot as plt


# 参数设置
lambda_wavelength = 632.8e-9  # 波长，单位：米 (632.8 nm)
sigma_values = np.linspace(1e-6, 10e-6, 100)  # 束腰半径σ范围：1μm 到 10μm


# 计算远场发散角 θ = λ / (πσ)
theta_values = lambda_wavelength / (np.pi * sigma_values)


# 绘图
plt.figure(figsize=(8, 5))
plt.plot(sigma_values * 1e6, theta_values * 1e3, 'b-', linewidth=2)
plt.xlabel('束腰半径 σ (μm)')
plt.ylabel('远场发散角 θ (mrad)')
plt.title('束腰半径对远场发散角的影响')
plt.grid(True)
plt.show()

此代码生成σ与θ的关系曲线，显示σ减小时θ的增大趋势。实际设计中，可用类似代码快速评估参数。

5. 关键点总结

以下思维导图概括高斯光束束腰与发散角关系的核心内容：

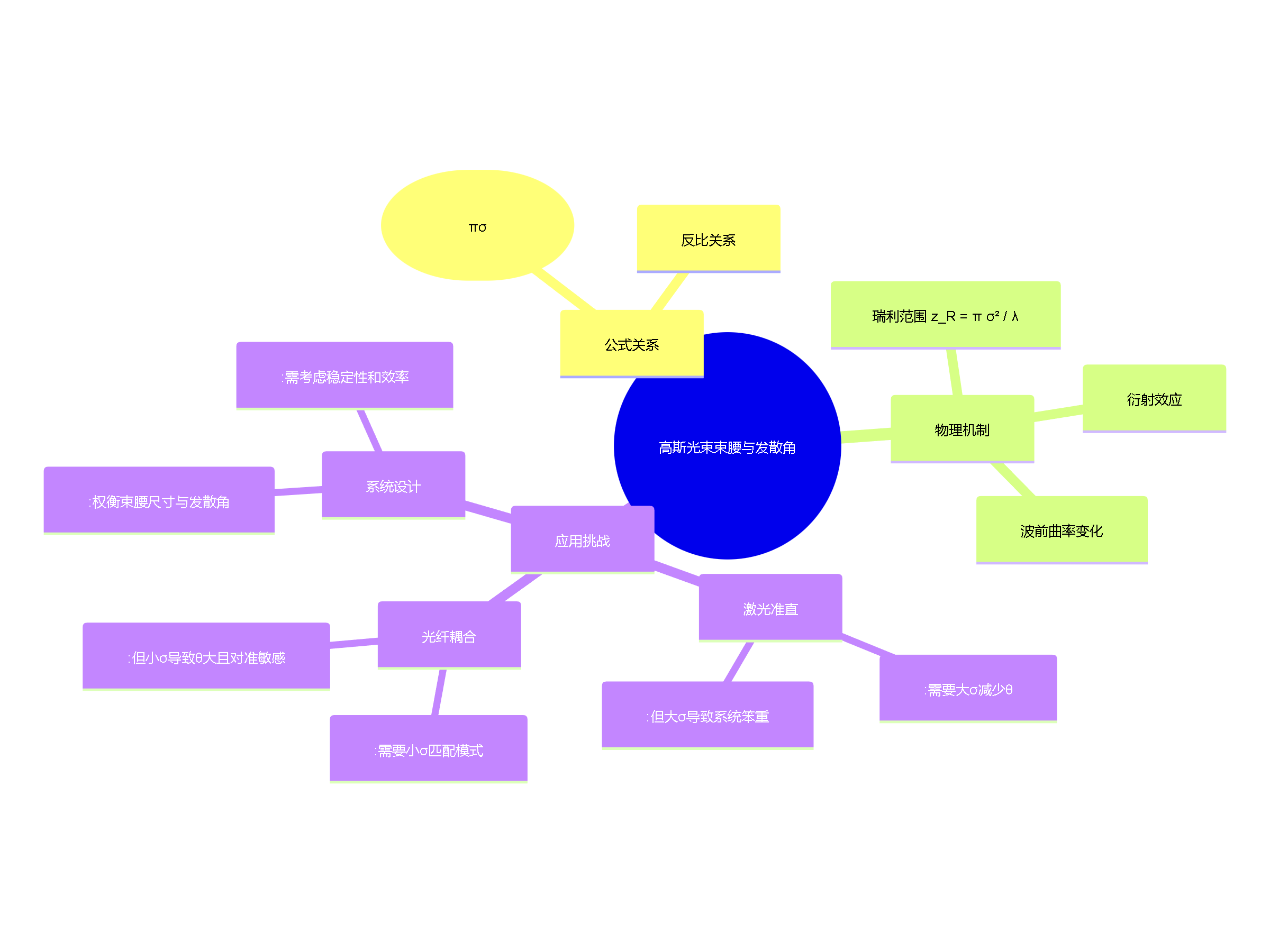
总之，束腰σ减小导致远场发散角θ增大是衍射效应的直接结果，在光学系统设计中需仔细平衡σ和θ，以优化性能。