麻烦写一下这个编程Stacks in C++

Question

Lab Objectives.
In this lab, you will practice what you had learned in Lecture 5 slides

Description of the Problem：
Stacks are used by compilers to help in the process of evaluating expressions and generating machine language code. In this exercise, we investigate how compilers evaluate arithm+c expressions consisting only of constants, operators and parenthese

Humans generally write expressions like 3 + 4 and 7 / 9 in which the operator (+ or / here) is written between its operands—this is called infix notation. Computers “prefer” postfix notation in which the operator is written to the right of its two operands. The preceding infix expressions would appear in postfix notation as 3 4 + and 7 9 /, respectively.

To evaluate a complex infix expression, a compiler would first convert the expression to postfix notation and evaluate the postfix version of the expression. Each of these algorithms requires only a single left-to-right pass of the expression. Each algorithm uses a stack object in support of its operation, and in each algorithm the stack is used for a different purpose.

In this exercise, you will write a C++ version of the infix-to-postfix conversion algorithm using both the the LinkedStackBag and LinkedArrayBag from Part A.

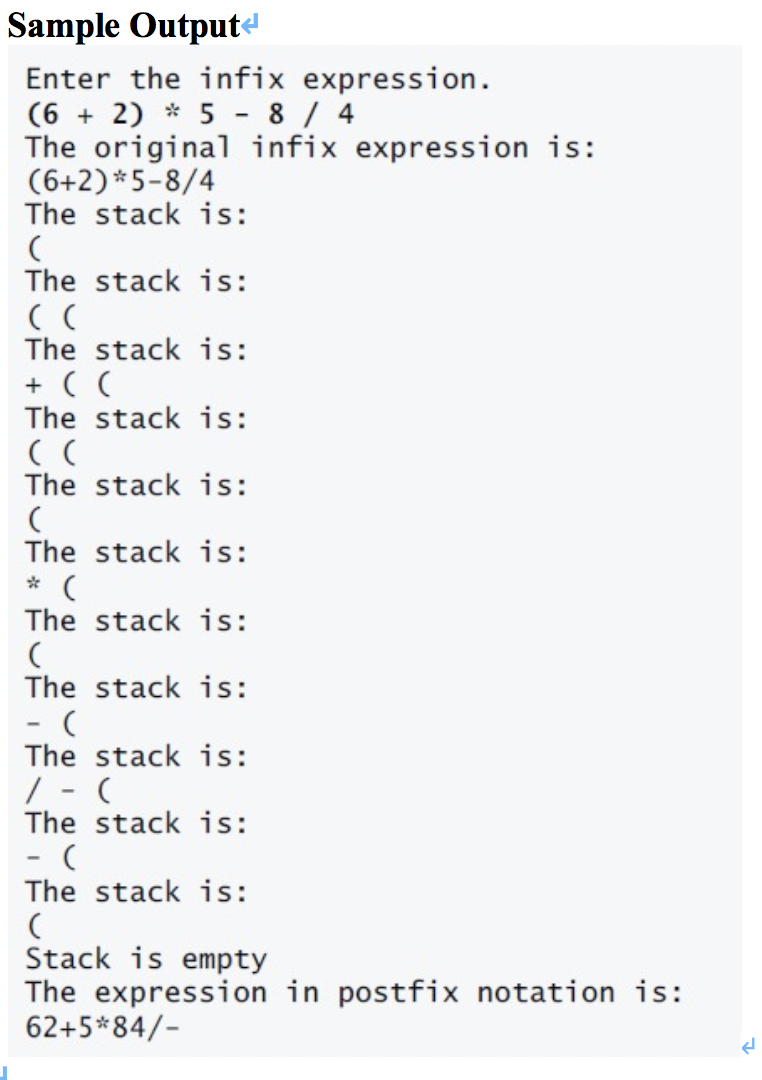
Please write a driver program that converts an ordinary infix arithmetic expression (assume a valid expression is entered) with single-digit integers such as (6 + 2) * 5 - 8 / 4 to a postfix expression. The postfix version of the preceding infix expression is 6 2 + 5 * 8 4 / -

The program should read the expression into character array infix and use modified versions of the stack functions implemented in this chapter to help create the postfix expression in character array postfix. The algorithm for creating a postfix expression is as follows:

• 1) Please push a left parenthesis '(' onto the stack.
• 2) Please append a right parenthesis ')' to the end of infix.
• 3) While the stack is not empty, please read infix from left to right and do the following:
• If the current character in infix is a digit, please copy it to the next element of postfix.
• If the current character in infix is a left parenthesis, please push it onto the stack.
• If the current character in infix is an operator,
• Please pop operators (if there are any) at the top of the stack while they have equal or higher precedence than the current operator, and please insert the popped operators in postfix.
• Please push the current character in infix onto the stack.

If the current character in infix is a right parenthesis
Please pop operators from the top of the stack and insert them in postfix until a left parenthesis is at the top of the stack.
Please pop (and discard) the left parenthesis from the stack.

The following arithmetic operations are allowed in an expression:

• addition
• subtraction
• multiplication
• / division
• ^ exponentiation
• % modulus

[Note: We assume left-to-right associativity for all operators for the purpose of this exercise.] The stack should be maintained with stack nodes, each containing a data member and a pointer to the next stack node.

Some of the functional capabilities you may want to provide are:

• a) function convertToPostfix that converts the infix expression to postfix notation
• b) function isOperator that determines whether c is an operator
• c) function precedence that determines whether the precedence of operator1 is less than, equal to or greater than the precedence of operator2 (the function returns –1, 0 and 1, respectively)
• d) function push that pushes a value onto the stack
• e) function pop that pops a value off the stack
• f) function stackTop that returns the top value of the stack without popping the stack
• g) function isEmpty that determines if the stack is empty
• h) function printStack that prints the stack

.

Answer 1

#include <iostream>
#include <stdio.h>
#include <cstring>
#include <stack>
#include <math.h>

using namespace std;

typedef double ElemType;
const int MaxSize = 100;
const int inf = 0x3f3f3f3f;

void trans(char *exp, char postexp[]);
double compvalue(char *postexp);

void filter(char * dest, char * src, char ch)
{
    int cur = 0;
    int i = 0; 
    while (src[i++] != '\0')
    {
        if (src[i - 1] == ch) continue;
        dest[cur++] = src[i - 1];
    }
    dest[cur] = '\0';
}

int main(void)
{
    char exp[MaxSize];
    char postexp[MaxSize];
    char postexp1[MaxSize];
    cout << "enter the infix expression." << endl;

    scanf("%[^\n]", exp);
    //strcpy(exp, "(6 + 2) * 5 - 8 / 4");

    filter(exp, exp, ' ');
    printf("the original infix expression is\n%s\n", exp);
    trans(exp, postexp);
    filter(postexp1, postexp, '#');
    cout << "the expression in postfix notation is:" << endl << postexp1 << endl;
    cout << "the value is:" << compvalue(postexp) << endl;


    return 0;
}

void printstack(stack<char> Optr)
{
    stack<char> temp;
    printf("the stack is:");
    if (Optr.empty())
    {
        printf("empty\n");
        return;
    }
    while (!Optr.empty())
    {
        temp.push(Optr.top());
        Optr.pop();
    }

    while (!temp.empty())
    {
        char c = temp.top();
        temp.pop();
        printf("%c ", c);
        Optr.push(c);
    }
    printf("\n");
}

void trans(char *exp, char postexp[])
{
    stack<char> Optr;
    int i = 0;
    char e;
    while (*exp != '\0')
    {
        switch (*exp)
        {
            case '(':
                Optr.push(*exp);
                printstack(Optr);
                exp++;
                break;
            case ')':
                e = Optr.top();
                Optr.pop();
                printstack(Optr);
                while (e != '(')
                {
                    postexp[i++] = e;
                    e = Optr.top();
                    Optr.pop();
                    printstack(Optr);
                }
                exp++;
                break;
            case '+':
            case '-':
                while (!Optr.empty())
                {
                    if (Optr.top() != '(')
                    {
                        e = Optr.top();
                        postexp[i++] = e;
                        Optr.pop();
                        printstack(Optr);
                    }
                    else
                        break;
                }
                Optr.push(*exp);
                printstack(Optr);
                exp++;
                break;
            case '*':
            case '/':
            case '%':
            case '^':
                while (!Optr.empty())
                {
                    if (Optr.top() == '*' || Optr.top() == '/' || Optr.top() == '%' || Optr.top() == '^')
                    {
                        e = Optr.top();
                        postexp[i++] = e;
                        Optr.pop();
                        printstack(Optr);
                    }
                    else
                        break;
                }
                Optr.push(*exp);
                printstack(Optr);
                exp++;
                break;
            default:
                while (*exp >= '0' && *exp <= '9')
                {
                    postexp[i++] = *exp;
                    exp++;
                }
                postexp[i++] = '#';
        }
    }
    while (!Optr.empty())
    {
        e = Optr.top();
        postexp[i++] = e;
        Optr.pop();
        printstack(Optr);
    }
    postexp[i] = '\0';
}

double compvalue(char *postexp)
{
    double d, a, b, c, e;
    stack<double> Opnd;
    while (*postexp != '\0')
    {
        switch (*postexp)
        {
            case '+':
                b = Opnd.top();
                Opnd.pop();
                a = Opnd.top();
                Opnd.pop();
                c = a+b;
                Opnd.push(c);
                break;
            case '-':
                b = Opnd.top();
                Opnd.pop();
                a = Opnd.top();
                Opnd.pop();
                c = a-b;
                Opnd.push(c);
                break;
            case '*':
                b = Opnd.top();
                Opnd.pop();
                a = Opnd.top();
                Opnd.pop();
                c = a*b;
                Opnd.push(c);
                break;
            case '/':
                b = Opnd.top();
                Opnd.pop();
                a = Opnd.top();
                Opnd.pop();
                if (b == 0)
                {
                    cout << "divide by zero!" << endl;
                    return inf;
                }
                else
                {
                    c = a/b;
                    Opnd.push(c);
                }
                break;
            case '%':
                b = Opnd.top();
                Opnd.pop();
                a = Opnd.top();
                Opnd.pop();
                if (b == 0)
                {
                    cout << "divide by zero!" << endl;
                    return inf;
                }
                else
                {
                    c = (int)a%(int)b;
                    Opnd.push(c);
                }
                break;
            case '^':
                b = Opnd.top();
                Opnd.pop();
                a = Opnd.top();
                Opnd.pop();
                c = pow(a,b);
                Opnd.push(c);
                break;
            default:
                d = 0;
                while (*postexp >= '0' && *postexp <= '9')
                {
                    d = d*10+*postexp-'0';
                    postexp++;
                }
                Opnd.push(d);
                break;
        }
        postexp++;
    }
    e = Opnd.top();
    Opnd.pop();
    return e;
}

https://ideone.com/50QE83

enter the infix expression.
(6 + 2) * 5 - 8 / 4
the original infix expression is
(6+2)*5-8/4
the stack is:(
the stack is:( +
the stack is:(
the stack is:empty
the stack is:*
the stack is:empty
the stack is:-
the stack is:- /
the stack is:-
the stack is:empty
the expression in postfix notation is:
62+5*84/-
the value is:38