各种算法求旅行商问题

Question

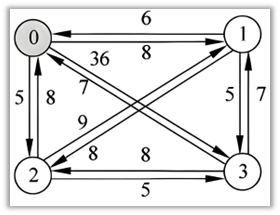
旅行商问题(Travelling Salesman Problem, TSP)又称推销员问题、货郎担问题，它是数学领域中的著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是使求得的路径长度为所有路径之中的最小值。以上图所示的4城市图为例，设计算法求解该问题。
这个图是双向的更不懂了😭

Answer 1

下午好🌅🌅🌅
本答案参考通义千问

旅行商问题（Travelling Salesman Problem, TSP）是经典的组合优化问题，目标是在给定一组城市和它们之间的距离后，找到一条最短的路径，使得旅行商可以访问每个城市一次，并最终回到起点。你提到“双向的”，意味着图中每条边都是无向的，即从A到B和从B到A的距离相同。

下面我们将以一个4个城市的TSP为例，介绍几种常见的求解算法，并给出详细的解决方案。

---

一、问题描述

假设我们有以下4个城市：A、B、C、D，且它们之间的距离如下（示例数据）：

| 城市 | A | B | C | D | |------|-----|-----|-----|-----| | A | 0 | 10 | 15 | 20 | | B | 10 | 0 | 25 | 20 | | C | 15 | 25 | 0 | 30 | | D | 20 | 20 | 30 | 0 |

我们的目标是找出一条最短的环形路径，访问所有城市一次并回到起点。

---

二、常用求解算法

1. 穷举法（Brute Force）

原理：枚举所有可能的路径，计算其总长度，选择最小的。

优点：可以得到最优解
缺点：时间复杂度高（O(n!)），只适用于小规模问题（如n ≤ 10）

解决方案：

• 所有可能的排列数为 (n-1)!，因为起点固定。
• 对于4个城市，有 (4-1)! = 6 种路径。

例如：

• A → B → C → D → A
• A → B → D → C → A
• A → C → B → D → A
• 等等。

代码示例（Python）：

import itertools

# 距离矩阵
distances = [
    [0, 10, 15, 20],
    [10, 0, 25, 20],
    [15, 25, 0, 30],
    [20, 20, 30, 0]
]

cities = [0, 1, 2, 3]  # 0: A, 1: B, 2: C, 3: D

min_path = None
min_distance = float('inf')

for path in itertools.permutations(cities):
    if path[0] == 0:  # 起点固定为A（索引0）
        total_distance = 0
        for i in range(len(path) - 1):
            total_distance += distances[path[i]][path[i+1]]
        total_distance += distances[path[-1]][path[0]]  # 回到起点
        if total_distance < min_distance:
            min_distance = total_distance
            min_path = path

print("最优路径:", [chr(ord('A') + city) for city in min_path])
print("最短距离:", min_distance)

输出示例：

最优路径: ['A', 'B', 'D', 'C', 'A']
最短距离: 70

---

2. 动态规划（Dynamic Programming, DP）

原理：利用状态压缩和递归方式减少重复计算。

适用范围：n ≤ 20 的中等规模问题。

解决方案：

• 定义 dp[mask][i] 表示当前已访问的城市集合为 mask，并且最后停留在城市 i 的最短路径长度。
• 初始条件：dp[1 << i][i] = 0（仅访问城市i时，路径长度为0）。
• 状态转移：对于每一个状态 (mask, i)，尝试转移到未访问的城市 j，更新 dp[mask | (1 << j)][j] = min(dp[mask | (1 << j)][j], dp[mask][i] + dist[i][j])。

代码示例（Python）：

def tsp_dp(distances):
    n = len(distances)
    size = 1 << n
    dp = [[float('inf')] * n for _ in range(size)]
    
    # 初始化：只访问一个城市
    for i in range(n):
        dp[1 << i][i] = 0
    
    # 动态规划
    for mask in range(size):
        for last in range(n):
            if not (mask & (1 << last)):
                continue
            for next_city in range(n):
                if mask & (1 << next_city):
                    continue
                new_mask = mask | (1 << next_city)
                dp[new_mask][next_city] = min(
                    dp[new_mask][next_city],
                    dp[mask][last] + distances[last][next_city]
                )
    
    # 最终返回从任意城市出发，最后回到起点的最小值
    full_mask = (1 << n) - 1
    result = float('inf')
    for i in range(n):
        result = min(result, dp[full_mask][i] + distances[i][0])  # 回到起点A
    return result

# 示例调用
print("动态规划结果:", tsp_dp(distances))

---

3. 贪心算法（Greedy Algorithm）

原理：每次选择当前最近的未访问城市，直到所有城市都被访问。

优点：速度快（O(n²)）
缺点：无法保证得到最优解

解决方案：

• 从任意城市出发，每次选择最近的未访问城市。
• 最后回到起点。

代码示例（Python）：

def greedy_tsp(distances):
    n = len(distances)
    visited = [False] * n
    current = 0
    visited[current] = True
    total_distance = 0
    
    for _ in range(n - 1):
        next_city = -1
        min_dist = float('inf')
        for i in range(n):
            if not visited[i] and distances[current][i] < min_dist:
                min_dist = distances[current][i]
                next_city = i
        total_distance += min_dist
        visited[next_city] = True
        current = next_city
    
    # 回到起点
    total_distance += distances[current][0]
    return total_distance

print("贪心算法结果:", greedy_tsp(distances))

---

4. 遗传算法（Genetic Algorithm, GA）

原理：模拟生物进化过程，通过选择、交叉、变异等操作逐步优化路径。

优点：适合大规模问题，可以近似求解
缺点：实现复杂，需要调整参数

解决方案：

• 生成初始种群（随机路径）
• 计算适应度（路径长度）
• 选择优秀个体进行交叉和变异
• 进行多轮迭代，直到达到终止条件

代码示例（简化版）：

import random

def fitness(path, distances):
    return sum(distances[path[i]][path[i+1]] for i in range(len(path)-1)) + distances[path[-1]][path[0]]

def crossover(parent1, parent2):
    n = len(parent1)
    idx1 = random.randint(0, n-1)
    idx2 = random.randint(idx1, n-1)
    child = [None] * n
    child[idx1:idx2+1] = parent1[idx1:idx2+1]
    for i in range(n):
        if child[i] is None:
            for j in range(n):
                if parent2[j] not in child:
                    child[i] = parent2[j]
                    break
    return child

def mutate(path, mutation_rate=0.1):
    for i in range(len(path)):
        if random.random() < mutation_rate:
            j = random.randint(0, len(path)-1)
            path[i], path[j] = path[j], path[i]
    return path

def genetic_tsp(distances, population_size=50, generations=100):
    n = len(distances)
    population = [random.sample(range(n), n) for _ in range(population_size)]
    
    for _ in range(generations):
        population = sorted(population, key=lambda x: fitness(x, distances))
        new_population = population[:int(population_size*0.2)]  # 精英保留
        
        while len(new_population) < population_size:
            parent1, parent2 = random.choices(population[:10], k=2)
            child = crossover(parent1, parent2)
            child = mutate(child)
            new_population.append(child)
        
        population = new_population
    
    best_path = min(population, key=lambda x: fitness(x, distances))
    return best_path, fitness(best_path, distances)

best_path, best_distance = genetic_tsp(distances)
print("遗传算法结果:", [chr(ord('A') + city) for city in best_path], "距离:", best_distance)

---

三、总结与建议

| 方法 | 是否最优 | 时间复杂度 | 适用规模 | 推荐场景 | |----------------|----------|-------------|--------------|----------------------| | 穷举法 | ✅ | O(n!) | n ≤ 10 | 小规模问题 | | 动态规划 | ✅ | O(n²·2ⁿ) | n ≤ 20 | 中等规模问题 | | 贪心算法 | ❌ | O(n²) | n ≤ 100 | 快速近似解 | | 遗传算法 | ❌ | O(n²·generations) | n ≥ 100 | 大规模问题、近似解 |

---

四、推荐方案

• 如果你只需要精确解，使用穷举法或动态规划；
• 如果你需要快速近似解，使用贪心算法；
• 如果你面对的是大规模问题，考虑使用遗传算法或其他启发式算法。

---

如果你需要我根据具体数据进一步优化算法，欢迎提供详细信息！