我下载了你的纯追踪法的代码,我发现你的代码结果图中圆圈的追踪轨迹的横向误差以及逆时针圆圈的追踪轨迹的横向误差在收敛的时候有着高频低幅震荡现象,还有就是S型轨迹的横向误差无法收敛。我是初学者,我想问一下这个这种现象是正常的吗?出现这种现象的原因是什么?能不能通过pid调参做到完美收敛?
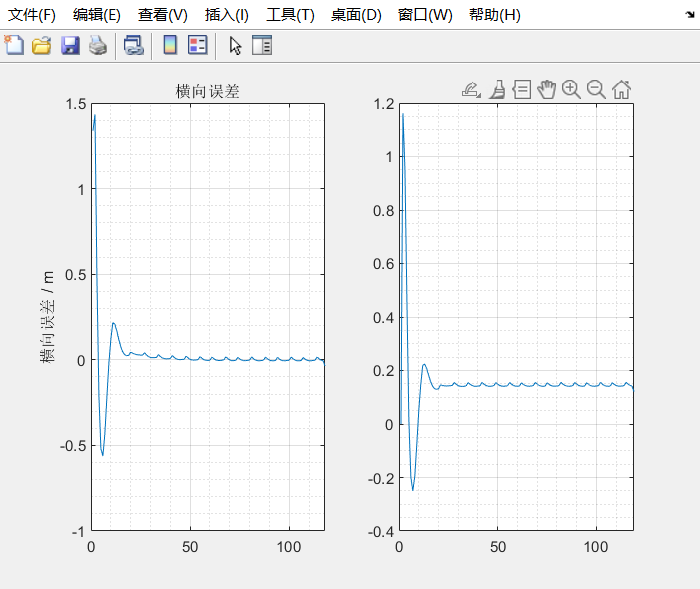
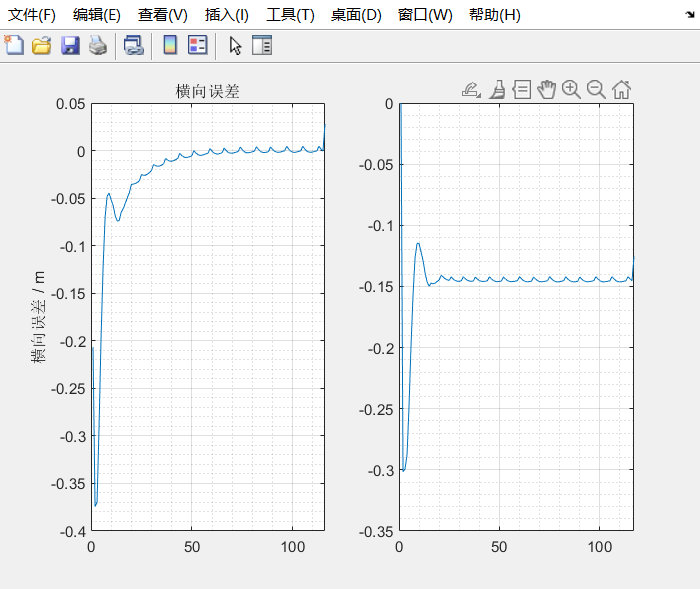
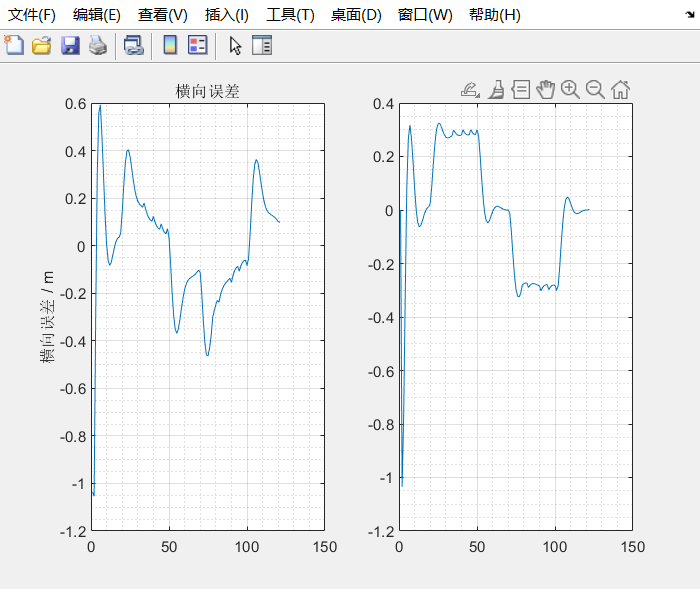
我下载了你的纯追踪法的代码,我发现你的代码结果图中圆圈的追踪轨迹的横向误差以及逆时针圆圈的追踪轨迹的横向误差在收敛的时候有着高频低幅震荡现象,还有就是S型轨迹的横向误差无法收敛。我是初学者,我想问一下这个这种现象是正常的吗?出现这种现象的原因是什么?能不能通过pid调参做到完美收敛?



下午好🌅🌅🌅
本答案参考通义千问
你的问题非常有代表性,涉及到纯追踪法(Pure Pursuit)在路径跟踪中的横向误差收敛性和轨迹形状对控制效果的影响。我们来逐步分析你提到的现象,并给出详细的解释与解决方案。
纯追踪法是一种经典的路径跟踪算法,其核心思想是:
它简单、易于实现,但也有明显的局限性,尤其是在复杂轨迹(如S型、圆圈)中容易出现横向误差无法收敛或高频震荡的问题。
这是正常的现象,原因如下:
重点:纯追踪法在圆弧路径中无法实现完美收敛,只能做到近似跟踪。
这个现象不正常,说明你的代码可能存在以下问题:
目标点选择不当:
参数设置不合理:
没有加入PID控制:
路径点密度不足:
lookahead_distance = max(5, curvature * 10) # 根据曲率自适应调整
# 定义PID参数
Kp = 0.8
Ki = 0.01
Kd = 0.1
# 计算横向误差
error = cross_track_error # 横向误差
# PID控制
control_output = Kp * error + Ki * integral_error + Kd * derivative_error
# 调整转向角度
steering_angle = pure_pursuit_angle + control_output
重点:PID控制能有效抑制高频震荡,提升系统稳定性。
| 问题 | 是否正常 | 原因 | 解决方案 | |------|----------|------|----------| | 圆圈轨迹横向误差高频震荡 | ✅ 正常 | 纯追踪法特性 | 不可完全消除,可通过PID优化 | | S型轨迹横向误差不收敛 | ❌ 不正常 | 目标点选择/参数/路径点密度 | 优化目标点、PID控制、增加路径点 | | 能否PID调参实现完美收敛? | ❌ 不能 | 系统固有特性 | 可显著改善,但不能完全消除 |
import math
def pure_pursuit(current_pos, target_path, lookahead_distance):
# 找到最近的路径点
nearest_index = find_nearest_point(current_pos, target_path)
# 选择目标点
if nearest_index + 1 < len(target_path):
target_point = target_path[nearest_index + 1]
else:
target_point = target_path[-1]
# 计算目标点与车辆的相对位置
dx = target_point[0] - current_pos[0]
dy = target_point[1] - current_pos[1]
angle_to_target = math.atan2(dy, dx)
# 计算横向误差
cross_track_error = math.sqrt(dx**2 + dy**2) * math.sin(angle_to_target - current_heading)
# PID 控制器
Kp = 0.8
Ki = 0.01
Kd = 0.1
control_output = Kp * cross_track_error + Ki * integral_error + Kd * (cross_track_error - last_error)
last_error = cross_track_error
# 计算最终转向角
steering_angle = angle_to_target + control_output
return steering_angle
如果你愿意,我可以进一步帮你调试你的代码,或者提供一个完整的仿真环境(如ROS、Gazebo、Python模拟器)来验证这些优化效果。欢迎继续提问!