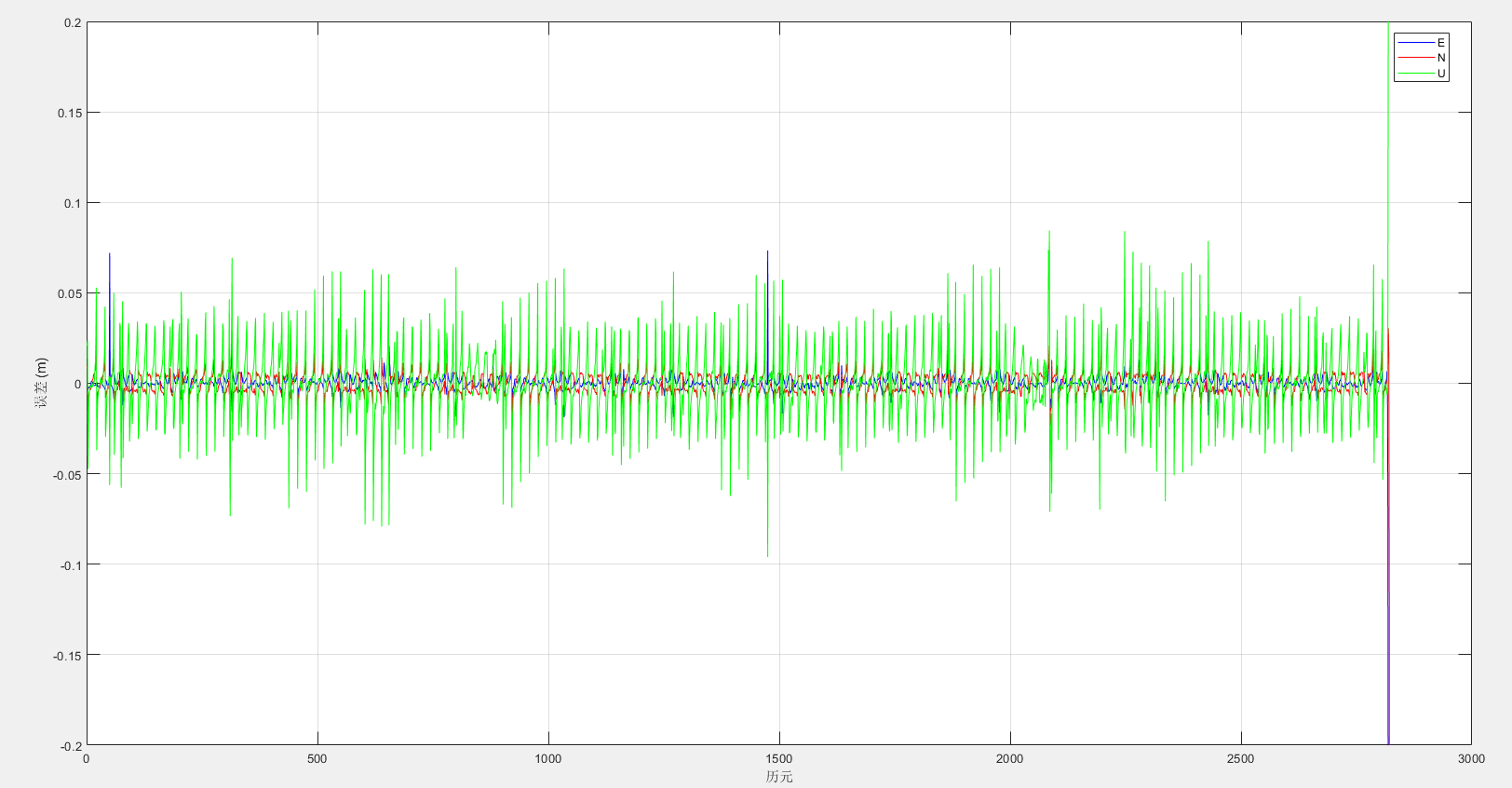
LEO仿真进行SPP，定位精度出现跳动

Question

#LEO仿真进行SPP精度出现规律性跳动

这是低轨伪距仿真的代码，各个误差模型按照SPP的设置
obs(1,3)=rho+recclk-satclkCLIGHT+ionalpha(satinfo(2),1)+trop+earthrotat-rel;

SPP定位误差呈现一定的规律性
现在的情况是earthrotat dts rel trop ion这几项用SPP最小二乘最后一次迭代算出来的参数和仿真用的相差很小，基本一样，卫星位置也基本一样（相差几毫米），但是有的历元求出来的rho（卫地距）和仿真对应的值差2个厘米，导致被接收机钟差吸收，接收机钟差变成2个厘米，实际仿真是0，我的理解是最小二乘没有收敛到最佳位置就停止迭代了

这是SPP最小二乘最后一次迭代

3 2017/09/01 00:00:59.989848 sat= 196 rs= -1024155.572   4879810.596   5989521.081 dts=     299.452 var=  0.000 svh=00
3 2017/09/01 00:00:59.993886 sat= 197 rs= -2711679.698   6742377.522   2826729.764 dts=     299.381 var=  0.000 svh=00
3 2017/09/01 00:00:59.990331 sat= 208 rs= -4880105.772   4304199.807   4293277.416 dts=     299.385 var=  0.000 svh=00
3 2017/09/01 00:00:59.991627 sat= 262 rs=  -571562.786   6385367.875   4435197.547 dts=     300.197 var=  0.000 svh=00
3 2017/09/01 00:00:59.993686 sat= 273 rs= -3786293.836   6127229.058   2986807.327 dts=     300.206 var=  0.000 svh=00
3 2017/09/01 00:00:59.988841 sat= 274 rs= -3258054.314   3601340.521   6094964.371 dts=     300.125 var=  0.000 svh=00

3 sat=196 azel=338.1  16.4 res=        0.002 P=  3043362.560 r+earthrotat=  3043649.751 r=  3043648.292 earthrotat=        1.459 dtr= -0.023 dts=      299.452 trop=  8.521 ion=  3.761 sig=1.899 varer=0.40851 vare= 0.000 vmeas=  0.090 vion=3.107 vtrp=0.090
3 sat=197 azel=194.9  45.9 res=       -0.002 P=  1832868.627 r+earthrotat=  1833162.241 r=  1833161.803 earthrotat=        0.438 dtr= -0.023 dts=      299.381 trop=  3.351 ion=  2.440 sig=1.270 varer=0.21528 vare= 0.000 vmeas=  0.090 vion=1.308 vtrp=0.090
3 sat=208 azel= 75.2  18.6 res=        0.003 P=  2898769.459 r+earthrotat=  2899056.850 r=  2899060.404 earthrotat=       -3.554 dtr= -0.023 dts=      299.385 trop=  7.550 ion=  4.464 sig=2.200 varer=0.37221 vare= 0.000 vmeas=  0.090 vion=4.377 vtrp=0.090
3 sat=262 azel=289.9  25.7 res=        0.001 P=  2510019.125 r+earthrotat=  2510310.714 r=  2510307.869 earthrotat=        2.845 dtr= -0.023 dts=      300.197 trop=  5.548 ion=  3.083 sig=1.573 varer=0.29737 vare= 0.000 vmeas=  0.090 vion=2.088 vtrp=0.090
3 sat=273 azel=138.9  43.4 res=        0.001 P=  1892789.127 r+earthrotat=  1893083.140 r=  1893084.351 earthrotat=       -1.211 dtr= -0.023 dts=      300.206 trop=  3.507 ion=  2.708 sig=1.386 varer=0.22109 vare= 0.000 vmeas=  0.090 vion=1.610 vtrp=0.090
3 sat=274 azel= 26.8  12.2 res=       -0.006 P=  3345316.592 r+earthrotat=  3345601.264 r=  3345603.233 earthrotat=       -1.969 dtr= -0.023 dts=      300.125 trop= 11.360 ion=  4.122 sig=2.083 varer=0.51464 vare= 0.000 vmeas=  0.090 vion=3.733 vtrp=0.090

这是仿真

2017/09/01 00:01:00.00000
L28 P=3043362.560 rho+earthrotat=3043649.730 rho=3043648.271 earthrotat=  1.459 dtr=  0.000 dts=     299.452 trop=  8.520 ion=  3.761 rs= -1024155.570 4879810.593 5989521.086
L29 P=1832868.627 rho+earthrotat=1833162.214 rho=1833161.776 earthrotat=  0.438 dtr=  0.000 dts=     299.380 trop=  3.351 ion=  2.441 rs= -2711679.696 6742377.520 2826729.771
L40 P=2898769.459 rho+earthrotat=2899056.827 rho=2899060.381 earthrotat= -3.554 dtr=  0.000 dts=     299.385 trop=  7.550 ion=  4.466 rs= -4880105.768 4304199.805 4293277.422
L94 P=2510019.125 rho+earthrotat=2510310.692 rho=2510307.847 earthrotat=  2.845 dtr=  0.000 dts=     300.197 trop=  5.547 ion=  3.083 rs= -571562.786 6385367.879 4435197.541
M05 P=1892789.127 rho+earthrotat=1893083.117 rho=1893084.328 earthrotat= -1.211 dtr=  0.000 dts=     300.206 trop=  3.507 ion=  2.709 rs= -3786293.836 6127229.061 2986807.321
M06 P=3345316.592 rho+earthrotat=3345601.234 rho=3345603.203 earthrotat= -1.969 dtr=  0.000 dts=     300.125 trop= 11.360 ion=  4.123 rs= -3258054.317 3601340.527 6094964.368

Answer 1

让 “紫雾凌寒” 来帮你回答,本回答结合 DeepSeek

如果还有问题，请评论或点击头像私信，如果有帮助到您, 请关注、采纳、点赞

1. 关键点分析：
   - 从提供的代码片段“obs(1,3)=rho+recclk-satclkCLIGHT+ionalpha(satinfo(2)”来看，问题可能出在以下几个方面。首先，不清楚各个变量的具体含义和取值范围是否合理，比如rho（伪距）、recclk（接收机时钟）、satclk（卫星时钟）、ionalpha(satinfo(2)等。其次，代码中没有看到关于误差模型的详细构建和处理过程，可能存在误差累积或模型不准确导致定位精度跳动。
2. 解决方案：
   - 明确变量含义和取值范围：
   • 仔细检查代码中每个变量的定义和计算方式，确保rho是准确测量的伪距值，recclk和satclk的计算是正确的，并且ionalpha(satinfo(2)的计算逻辑合理。例如，如果rho是通过某种测量算法得到的，要检查该算法的准确性和稳定性。
   • 详细分析误差模型：
   • 对于每个误差项，如卫星时钟误差、接收机时钟误差、电离层误差等，要深入研究其模型。比如卫星时钟误差可能与卫星的轨道、星载原子钟的特性等有关。可以考虑使用更精确的卫星时钟误差模型，如国际 GNSS 服务（IGS）提供的卫星时钟改正数据。
   • 对于电离层误差ionalpha(satinfo(2)，可以采用更复杂的电离层模型，如 Klobuchar 模型等。以下是一个简单的 Klobuchar 模型示例代码（假设已经有相关的输入参数计算出了模型所需的参数）：

% Klobuchar 电离层延迟模型示例
% 假设已经计算出了相关参数
% 输入参数：
%  - phi: 纬度
%  - lambda: 经度
%  - time: 时间（秒）
%  - A: Klobuchar 模型参数 A
%  - B: Klobuchar 模型参数 B
%  - C: Klobuchar 模型参数 C
%  - D: Klobuchar 模型参数 D
%  - E: Klobuchar 模型参数 E
%  - F: Klobuchar 模型参数 F

phi = 30; % 示例纬度
lambda = 120; % 示例经度
time = 3600 * 12; % 示例时间（中午 12 点）
A = 5e-9;
B = 1e-9;
C = 1e-9;
D = 1e-9;
E = 1e-9;
F = 1e-9;

% 计算电离层延迟
ion_delay = A + B * cos(2 * pi * (time - 50400) / 2419200) + C * sin(2 * pi * (time - 50400) / 2419200) + D * cos(4 * pi * (time - 50400) / 2419200) + E * sin(4 * pi * (time - 50400) / 2419200) + F * cos(6 * pi * (time - 50400) / 2419200);

• 增加数据平滑处理：
  • 可以使用滤波算法对定位结果进行平滑处理，减少跳动。例如，简单的移动平均滤波。假设定位结果存储在一个向量position中：

% 移动平均滤波示例
window_size = 5; % 窗口大小
filtered_position = movmean(position, window_size);

1. 多种解决方案的优缺点：
   - 明确变量含义和取值范围：
   • 优点：从根本上解决问题，如果变量本身不准确，修正后可以大大提高定位精度。
   • 缺点：需要对整个代码中变量的计算和定义进行全面审查，工作量较大。
   • 详细分析误差模型：
   • 优点：通过改进误差模型，可以更准确地模拟实际情况，提高定位精度。
   • 缺点：不同的误差模型可能需要更多的参数和数据支持，实现起来相对复杂。
   • 增加数据平滑处理：
   • 优点：简单易行，可以快速减少定位精度的跳动。
   • 缺点：只是对结果进行了平滑，不能从根本上解决误差模型不准确的问题，如果误差过大，平滑效果可能有限。
2. 总结：
   - 要解决LEO仿真进行SPP定位精度出现跳动的问题，需要从多个方面入手。首先要确保代码中各个变量的准确性和合理性，然后深入分析误差模型并进行改进，最后可以通过数据平滑处理来减少跳动。综合运用这些方法，有望提高定位精度的稳定性。

请注意，以上代码示例仅为示意，实际应用中需要根据具体的LEO仿真和SPP算法进行调整和完善。

希望以上解答对您有所帮助。如果您有任何疑问，欢迎在评论区提出。