c++三维渲染小数点困惑

Question

#include <graphics.h>
#include <cmath>
#include <vector>
#include<stdio.h>
#include<easyx.h>

// 定义三维点
struct Point3D {
    double x, y, z;
    Point3D(double x = 0, double y = 0, double z = 0) : x(x), y(y), z(z) {}
};

// 定义二维点（屏幕坐标）
struct Point2D {
    int x, y;
    Point2D(int x = 0, int y = 0) : x(x), y(y) {}
};

// 球体参数
const double PI = 3.1415926535;
const int radius = 150;          // 球体半径
const int centerX = 400;         // 屏幕中心 X 坐标
const int centerY = 300;         // 屏幕中心 Y 坐标
const int stacks = 30;           // 经线（纬度圈）数量，越多越精细
const int slices = 30;           // 纬线（经度圈）数量，越多越精细

// 存储所有顶点的三维坐标和投影后的二维坐标
std::vector<std::vector<Point3D>> vertices3D;
std::vector<std::vector<Point2D>> vertices2D;

// 旋转角度
double angleX = 0, angleY = 0, angleZ = 0;

// 三维旋转函数 (绕X轴)
Point3D rotateX(const Point3D& p, double angle) {
    double cosA = cos(angle), sinA = sin(angle);
    return Point3D(p.x, p.y * cosA - p.z * sinA, p.y * sinA + p.z * cosA);
}

// 三维旋转函数 (绕Y轴)
Point3D rotateY(const Point3D& p, double angle) {
    double cosA = cos(angle), sinA = sin(angle);
    return Point3D(p.x * cosA + p.z * sinA, p.y, -p.x * sinA + p.z * cosA);
}

// 三维旋转函数 (绕Z轴)
Point3D rotateZ(const Point3D& p, double angle) {
    double cosA = cos(angle), sinA = sin(angle);
    return Point3D(p.x * cosA - p.y * sinA, p.x * sinA + p.y * cosA, p.z);
}

// 初始化球体顶点
void initSphere() {
    vertices3D.resize(stacks + 1);
    for (int i = 0; i <= stacks; ++i) {
        vertices3D[i].resize(slices + 1);
        double theta = PI * i / stacks;          // 极角 (0 到 PI)
        double sinTheta = sin(theta);
        double cosTheta = cos(theta);

        for (int j = 0; j <= slices; ++j) {
            double phi = 2 * PI * j / slices;    // 方位角 (0 到 2PI)
            double sinPhi = sin(phi);
            double cosPhi = cos(phi);

            // 你提供的第一组公式就在这里！
            double x = radius * sinTheta * cosPhi;
            double y = radius * sinTheta * sinPhi;
            double z = radius * cosTheta;

            vertices3D[i][j] = Point3D(x, y, z);
        }
    }
}

// 投影并绘制
void draw() {
    // 应用旋转并投影到2D
    for (int i = 0; i <= stacks; ++i) {
        for (int j = 0; j <= slices; ++j) {
            Point3D p = vertices3D[i][j];
            // 应用旋转
            p = rotateX(p, angleX);
            p = rotateY(p, angleY);
            p = rotateZ(p, angleZ);
            // 平行投影到2D (忽略Z)，并平移到屏幕中心
            int screenX = centerX + static_cast<int>(p.x);
            int screenY = centerY + static_cast<int>(p.y);
            vertices2D[i][j] = Point2D(screenX, screenY);
        }
    }

    // 绘制经线 (连接纬度圈上的点)
    for (int i = 0; i < stacks; ++i) {
        for (int j = 0; j < slices; ++j) {
            // 绘制四边形，这里简化为绘制两条线来形成网格
            line(vertices2D[i][j].x, vertices2D[i][j].y,
                vertices2D[i][j + 1].x, vertices2D[i][j + 1].y);
            line(vertices2D[i][j].x, vertices2D[i][j].y,
                vertices2D[i + 1][j].x, vertices2D[i + 1][j].y);
        }
        // 绘制最后一根经线
        line(vertices2D[i][slices].x, vertices2D[i][slices].y,
            vertices2D[i + 1][slices].x, vertices2D[i + 1][slices].y);
    }
    // 绘制最后一圈纬线
    for (int j = 0; j < slices; ++j) {
        line(vertices2D[stacks][j].x, vertices2D[stacks][j].y,
            vertices2D[stacks][j + 1].x, vertices2D[stacks][j + 1].y);
    }
}

int main() {
    // 创建绘图窗口
    initgraph(1800, 1600);
    // 设置坐标原点为左上角 (EasyX默认)，y轴向下为正。我们已经在draw函数中手动处理了屏幕中心和平移。
    // 如果想用标准的数学坐标系，可以取消下面的注释
    // setorigin(centerX, centerY); // 设置原点为屏幕中心
    // setaspectratio(1, -1);       // 翻转y轴，使其向上为正

    initSphere();
    // 为投影后的2D点分配空间
    vertices2D.resize(stacks + 1);
    for (int i = 0; i <= stacks; ++i) {
        vertices2D[i].resize(slices + 1);
    }

    // 游戏主循环
    BeginBatchDraw(); // 开始批量绘图，防止闪烁
    while (1) { // 按下任意键退出
        cleardevice();

        // 更新旋转角度
        angleX += 0.01;
        angleY += 0.02;
        // angleZ += 0.005;

        // 绘制球体
        setlinecolor(WHITE); // 设置线条颜色为白色
        draw();

        FlushBatchDraw(); // 刷新画布，显示绘制内容
        Sleep(10);        // 短暂延时，控制帧率
    }
    EndBatchDraw();       // 结束批量绘图
    closegraph();         // 关闭窗口
    return 0;
}

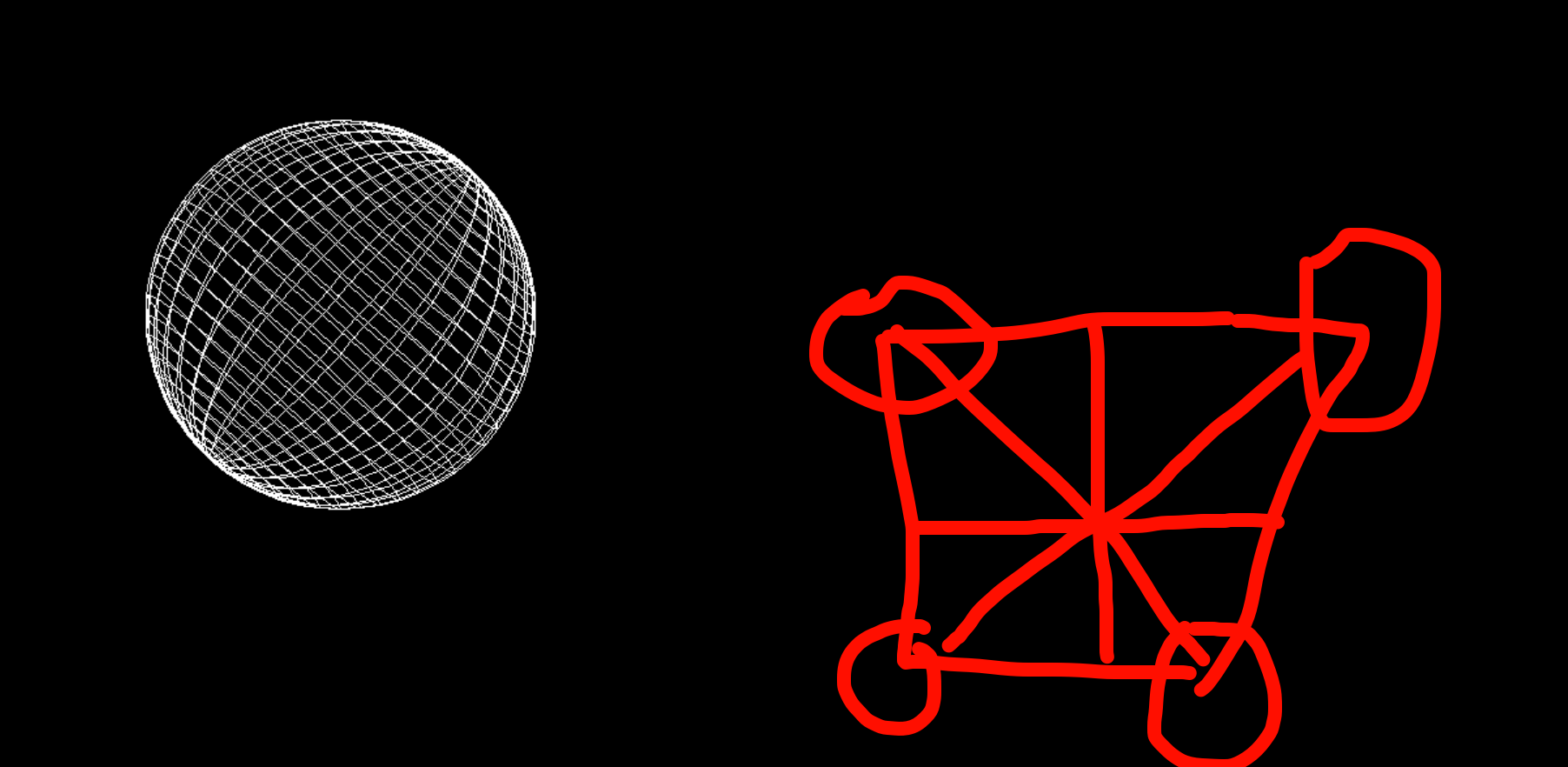
疑问为什么用easyx无法对两条直线的那个交点进行颜色渲染

Answer 1

我是YJlio杨利杰让我来给你回答，以下回答来自ChatGpt5.2 Thinking 深度思考

结论

你这个“C++ 三维渲染小数点困惑”，在 3D 渲染里最常见的坑其实就两类：

1. 小数被截断/精度丢失（比如用了 int、或 1/2 这种整数除法）；
2. 显示/输出格式导致你以为数值不对（比如打印默认精度太低，或 ImGui/日志只显示两位小数）。
   正文未识别，我无法断言你具体是哪一种，但你按下面步骤排查，基本能把问题定位到“计算错”还是“显示错”。

原因

1）整数除法导致小数“变 0”

C++ 里 1/2 是 整数除法，结果是 0，即便赋值给 float 也是 0.0：

float a = 1/2;   // 0.0  (因为 1/2 先算成 0)
float b = 1.0f/2; // 0.5 (正确)

在渲染里常见于：归一化、插值、进度、uv、比例缩放、FOV 计算等。

2）用错类型：int/short/uint 导致截断

例如你做坐标变换时本应是 float/double，却中间用 int 接了一下：

float x = 1.9f;
int xi = x;      // 1  (截断)
float y = xi;    // 1.0f  (精度已经丢了)

渲染里常见于：屏幕坐标、像素坐标、矩阵计算中间变量、顶点数据布局（VAO/VBO）传错类型。

3）浮点精度问题（float 精度有限）

• float 大约 7 位十进制有效数字，坐标值很大时，小数会“抖动/丢位”（典型：大世界坐标、摄像机远离原点）。
• 解决：核心计算用 double 或做 Floating Origin（浮动原点）。

4）显示精度误导（你以为是“算错”，其实只是“打印少”）

默认 std::cout 输出精度可能让你看不出差别：

#include <iostream>
#include <iomanip>

double v = 0.123456789;
std::cout << v << "\n";                    // 可能只显示 0.123457
std::cout << std::fixed << std::setprecision(9) << v << "\n"; // 0.123456789

5）矩阵/坐标系单位混用（角度/弧度）

“看起来像小数不对”，实际是单位错：

• sin/cos/tan 用 弧度，你传了角度会导致结果离谱。

步骤（按顺序做，最快定位）

1）先把“关键变量”用高精度打印出来

#include <iostream>
#include <iomanip>

auto P = [](const char* name, double v){
    std::cout << name << " = " << std::fixed << std::setprecision(12) << v << "\n";
};

把你困惑的变量（坐标、矩阵元素、插值系数 t、缩放比例等）都打印一遍，判断是计算阶段就错，还是显示阶段误导。

2）全局搜索“可疑整数除法”

重点搜：/ 2、/ 255、/ width、/ height、(a-b)/(c-d) 等，检查是否两边都是整数。
修正方式：至少一边转成浮点：

float t = (float)i / (float)n;
// 或
float t = i / (n * 1.0f);

3）检查中间变量类型是否被 int 吃掉

特别是这类链式写法：

auto sx = (w / 2) * scale;   // w 是 int 会先做整数除法
auto sx = (w * 0.5f) * scale; // 正确

4）检查顶点数据传入 GPU 的类型/步长是否正确（渲染常见隐性坑）

比如你 CPU 侧是 float，但 OpenGL/DirectX 侧声明成了 int/short 或 stride/offset 错，会出现坐标“小数像丢了”。
（由于你没贴 API，我只给通用检查项）

• 顶点结构体里 position/normal/uv 是否是 float
• sizeof(Vertex) 是否匹配 stride
• attribute 指定类型是否是 FLOAT

5）大坐标场景：用 double 或浮动原点

如果你的坐标已经到 1e6、1e7 级别，float 的小数会明显不稳定。
快速验证：把同一段计算改成 double 看是否稳定：

double x = ...;
double y = ...;
double z = ...;

验证（你按这几条确认“真修好”）

1. 同一输入下，关键变量打印出来的小数位是否符合预期（至少 6~12 位）
2. 将变量强制改成 float/double 两种实现对比，差异是否可解释（float 有误差，double 更稳定）
3. 若是渲染显示问题：CPU 打印正确，但屏幕显示不对 → 重点查“顶点传输/矩阵/坐标系/单位”

补充

因为正文未识别，我没法直接对你那段代码“定点爆破”。你只要贴出以下任意一种信息，我就能把答案从“通用排查”变成“精准修复”：

• 你困惑的那段计算代码（10~30 行）
• 你打印出来的几组输入输出（比如原始坐标、变换后的坐标、最终屏幕坐标）
• 你用的是 OpenGL/DirectX/自研软件渲染/某个引擎（以及顶点格式定义）

另外给一个最小自检例子（很多人就是这里踩坑）：

int w = 1920;
float half = w / 2;      // 960.0 还行，但如果是 w/2*scale 可能先截断
float u = 1 / 255;       // 0.0  (错)
float u2 = 1.0f / 255.0f; // 0.0039215686 (对)