程序是数据结构的图的存储和遍历实验,功能是输入一个无向图并将其转换成邻接矩阵,然后把邻接矩阵变成邻接表,最后深度优先遍历该邻接表生成树(VS2017):
#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
#include <string.h>
#include<iostream>
using namespace std;
typedef int InfoType;
#define MAXV 100 //最大顶点个数
#define INF 32767 //INF表示∞
#define isLetter(a) ((((a)>='a')&&((a)<='z')) || (((a)>='A')&&((a)<='Z')))
#define LENGTH(a) (sizeof(a)/sizeof(a[0]))
//以下定义邻接矩阵类型
typedef struct
{
int no; //顶点编号
InfoType info; //顶点其他信息
} VertexType; //顶点类型
typedef struct //图的定义
{
char vexnum[MAXV];
int edges[MAXV][MAXV]; //邻接矩阵
int n, e; //顶点数,边数
VertexType vexs[MAXV]; //存放顶点信息
} MGraph, *PGragh; //图的邻接矩阵类型
//以下定义邻接表类型
typedef struct ANode //边的节点结构类型
{
int adjvex; //该边的终点位置
struct ANode *nextarc = NULL; //指向下一条边的指针
InfoType *info; //该边的相关信息,这里用于存放权值
} ArcNode;
typedef int Vertex;
typedef struct Vnode //邻接表头节点的类型
{
Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode;
typedef VNode AdjList[MAXV]; //AdjList是邻接表类型
typedef struct
{
AdjList adjlist; //邻接表
int n, e; //图中顶点数n和边数e
} ALGraph; //图的邻接表类型
void MatToList(MGraph *g, ALGraph *G)
//将邻接矩阵g转换成邻接表G
{
int i, j;
ArcNode *p;
//G = (ALGraph *)malloc(sizeof(ALGraph));
for (i = 0; i<g->n; i++) //给邻接表中所有头节点的指针域置初值
G->adjlist[i].firstarc = NULL;
for (i = 0; i<g->n; i++) //检查邻接矩阵中每个元素
for (j = g->n - 1; j >= 0; j--)
if (g->edges[i][j] != 0) //存在一条边
{
p = (ArcNode *)malloc(sizeof(ArcNode)); //创建一个节点*p
p->adjvex = j;
p->nextarc = G->adjlist[i].firstarc; //采用头插法插入*p
G->adjlist[i].firstarc = p;
}
G->n = g->n; G->e = g->e;
//return G;
}
void DispMat(MGraph *g)
//输出邻接矩阵g
{
int i, j;
for (i = 0; i<g->n; i++)
{
for (j = 0; j<g->n; j++)
printf("%3d", g->edges[i][j]);
printf("\n");
}
}
void DispAdj(ALGraph G)
//输出邻接表G
{
int i;
ArcNode *p;
for (i = 0; i<G.n; i++)
{
p = G.adjlist[i].firstarc;
printf("%3d: ",i);
//cout << i << ":";
while (p != NULL)
{
//printf("%3d",p->adjvex);
cout << p->adjvex << " ";
p = p->nextarc;
}
printf("\n");
}
}
static int get_position(MGraph g, char ch)
{
int i;
for (i = 0; i<g.n; i++)
if (g.vexnum[i] == ch)
return i;
return -1;
}
//读取一个输入字符
static char read_char()
{
char ch;
do {
ch = getchar();
} while (!isLetter(ch));
return ch;
}
// 创建无向图
MGraph* create_graph()
{
char c1, c2;
int vex, edge;
int i, p1, p2;
MGraph* pG;
// 输入顶点数和边数
printf("输入顶点数和边数:");
scanf_s("%d%d", &vex, &edge);
if (vex < 1 || edge < 1 || (edge >(vex * (vex - 1))))
{
printf("input error: invalid parameters!\n");
return NULL;
}
if ((pG = (MGraph*)malloc(sizeof(MGraph))) == NULL)
return NULL;
memset(pG, 0, sizeof(MGraph));
// 初始化顶点数和边数
pG->n = vex;
pG->e = edge;
// 初始化"顶点"
printf("输入各顶点名称:\n");
for (i = 0; i < pG->n; i++)
{
printf("vertex(%d): ", i);
pG->vexnum[i] = read_char();
}
// 初始化"边"
for (i = 0; i < pG->e; i++)
{
// 读取边的起始顶点和结束顶点
printf("edge(%d):", i);
c1 = read_char();
c2 = read_char();
p1 = get_position(*pG, c1);
p2 = get_position(*pG, c2);
if (p1 == -1 || p2 == -1)
{
printf("input error: invalid edge!\n");
free(pG);
return NULL;
}
pG->edges[p1][p2] = 1;
pG->edges[p2][p1] = 1;
}
return pG;
}
// 打印矩阵队列图
void print_graph(MGraph G)
{
int i, j;
printf("Martix Graph:\n");
for (i = 0; i < G.n; i++)
{
for (j = 0; j < G.n; j++)
printf("%d ", G.edges[i][j]);
printf("\n");
}
}
//创建一个树的左子女,右兄弟结构
typedef struct node
{
int data;
node *firstChild = NULL;
node *nextSibling = NULL;
}TreeNode, *BinTree;
int visited[MAXV];
void Dfs(ALGraph G, int i, BinTree &T)
{
visited[i] = 1;
bool first = true;//表示是否为当前节点第一个孩子
TreeNode *locat = new TreeNode;//同样是定位作用
while (G.adjlist[i].firstarc != NULL)//从此节点出发,访问邻接节点。
{
if (visited[G.adjlist[i].firstarc->adjvex] == 0)
{
visited[G.adjlist[i].firstarc->adjvex] = 1;
TreeNode *t = new TreeNode;//建立一颗小树
t->data = G.adjlist[i].firstarc->adjvex;
if (first)//是当前节点第一个孩子
{
T->nextSibling = t;//建立右孩子
first = false;//表示不是传进来的第一个孩子,则是孩子们的兄弟
}
else
{
locat->nextSibling = t;
}
locat = t;
Dfs(G, G.adjlist[i].firstarc->adjvex, t);//继续对小树找兄弟
}
G.adjlist[i].firstarc = G.adjlist[i].firstarc->nextarc;
}
}
void DFS_Traverse(ALGraph G, BinTree &T)
{
TreeNode *locat = new TreeNode;//此处定义一个定位指针,用来定位当前树的位置
for (int i = 1; i <= G.n; i++)
{
visited[i] = 0;
}
for (int i = 1; i <= G.n; i++)
{
if (visited[i] == 0)
{
TreeNode *t = new TreeNode;//这代表一个小树
t->data = G.adjlist[i].data;
if (T == NULL)
{
T = t;//若树为空,建立头节点
}
else
{
locat->nextSibling = t;//若树不空,则是森林,插入右兄弟
}
locat = t;//定位至小树
Dfs(G, i, locat);//建立小树
}
}
}
//建立图深度优先搜索森林
void DFSForest(ALGraph G, BinTree &T)
{
DFS_Traverse(G, T);
}
void Display(BinTree T)
{
if (T)
{
cout << T->data << ' ';
Display(T->firstChild);
Display(T->nextSibling);
}
}
//以下主函数用作调试
int main()
{
//int i, j;
MGraph* g, g1;
ALGraph G;
BinTree T;
g = create_graph();
printf("\n");
printf(" 无向图G的邻接矩阵:\n");
DispMat(g);
//G = (ALGraph *)malloc(sizeof(ALGraph));
//M = (ALGraph *)malloc(sizeof(ALGraph));
printf(" 图G的邻接矩阵转换成邻接表,顶点名称用编号表示:\n");
MatToList(g, &G);
DispAdj(G);
DFSForest(G, T);
Display(T);
system("pause");
}
运行程序,输入顶点和边的信息,能够输出邻接矩阵和邻接表,但到了生成森林那一步就报异常: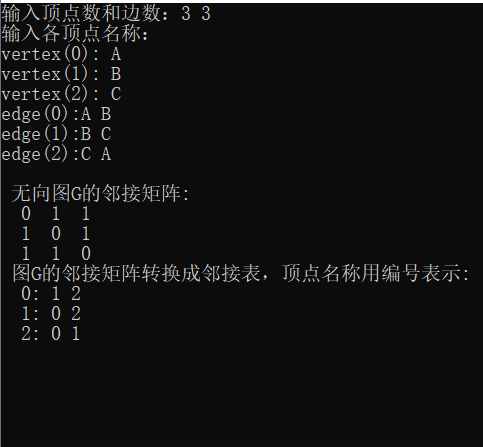
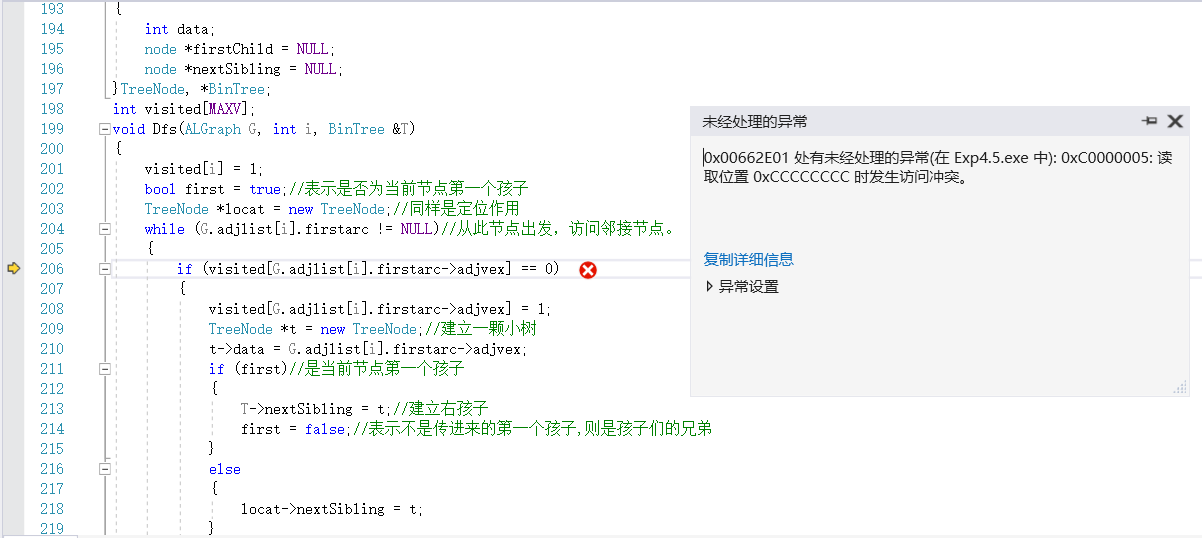
和同学研究了一下发现问题可能是出在执行到函数
void DFS_Traverse(ALGraph G, BinTree &T)
{
TreeNode *locat = new TreeNode;//此处定义一个定位指针,用来定位当前树的位置
for (int i = 1; i <= G.n; i++)
{
visited[i] = 0;
}
for (int i = 1; i <= G.n; i++)
{
if (visited[i] == 0)
{
TreeNode *t = new TreeNode;//这代表一个小树
t->data = G.adjlist[i].data;
if (T == NULL)
{
T = t;//若树为空,建立头节点
}
else
{
locat->nextSibling = t;//若树不空,则是森林,插入右兄弟
}
locat = t;//定位至小树
Dfs(G, i, locat);//建立小树
}
}
}
的最后一个for中的Dfs(G,i,locat);这一句时出了问题,若在该处设置断点再重新运行程序并输入测试数据: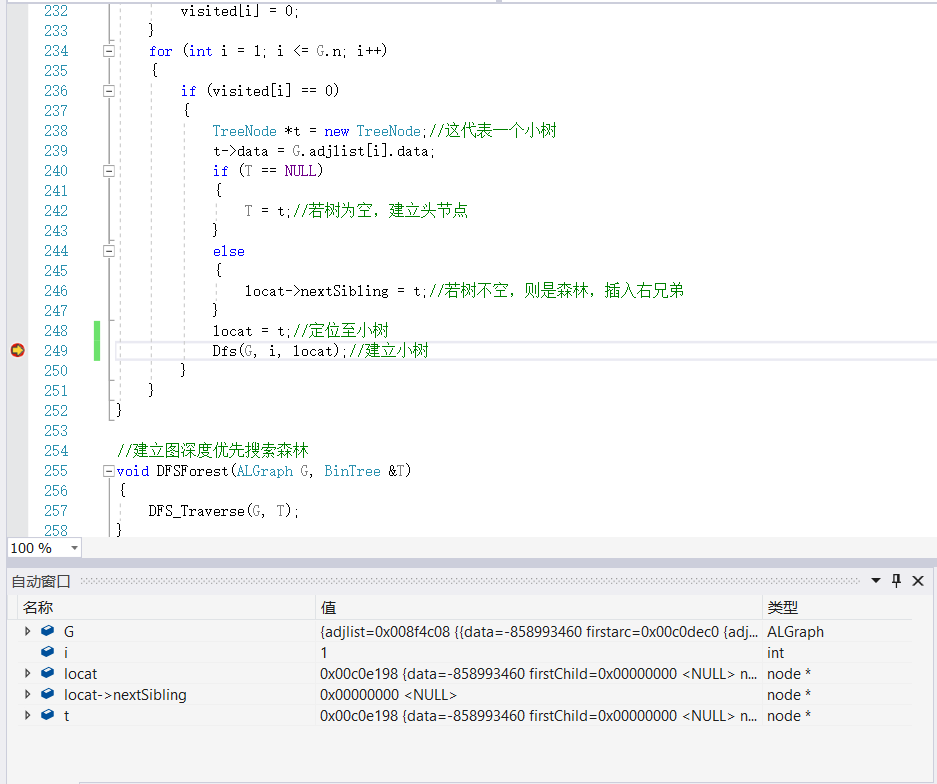
然后按F11逐行运行,就跳到了函数Dfs()那里: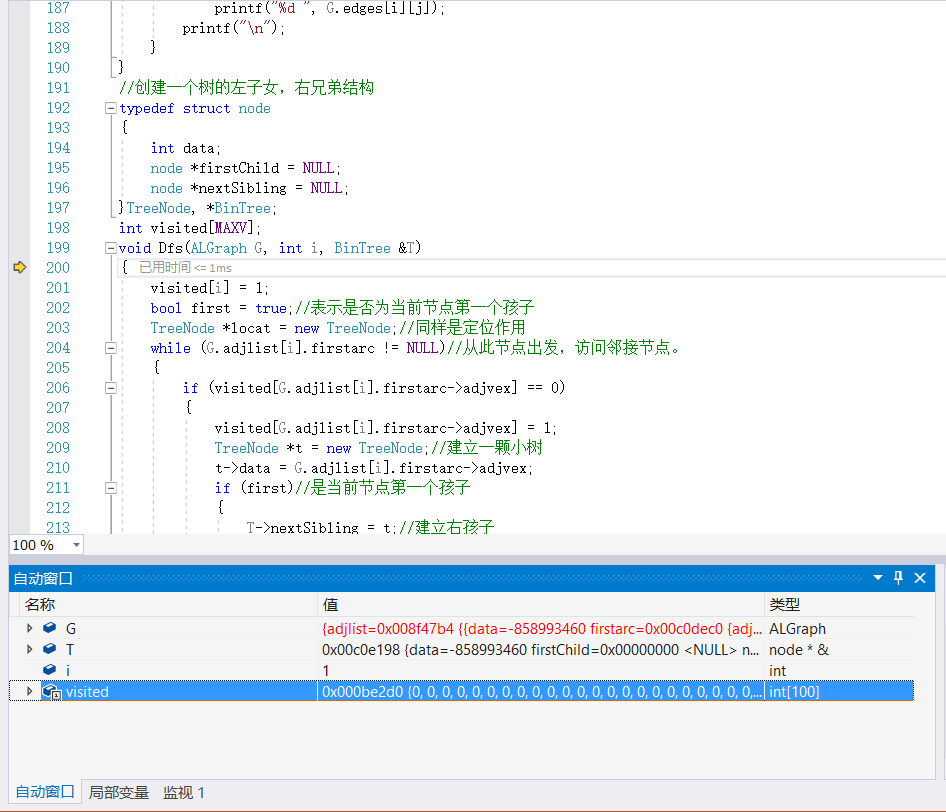
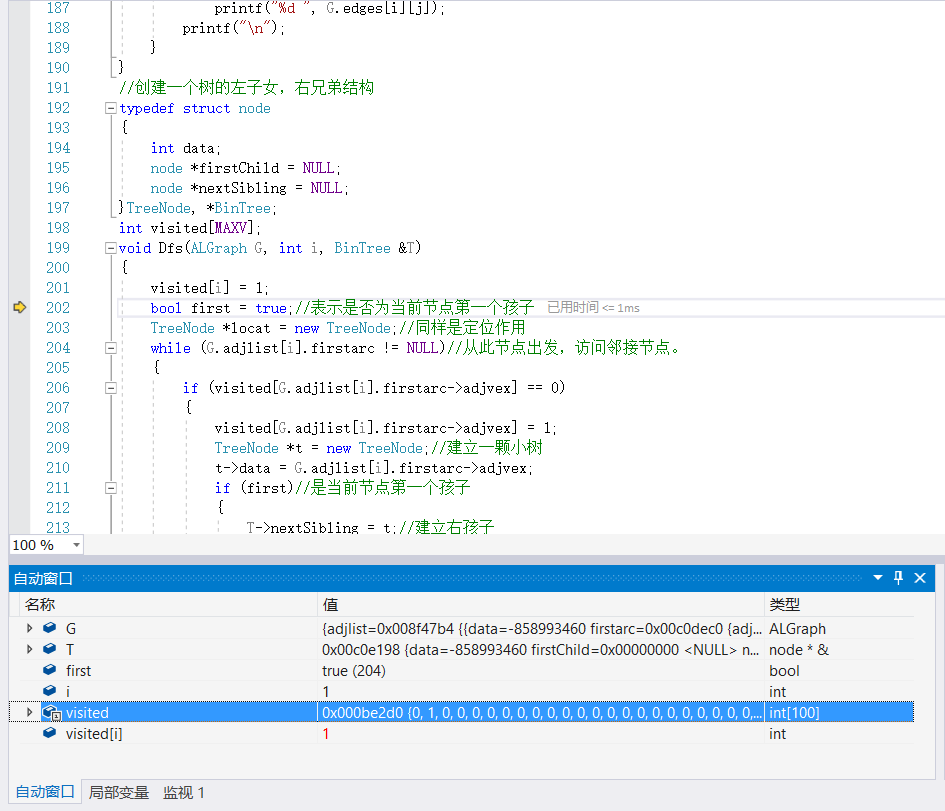
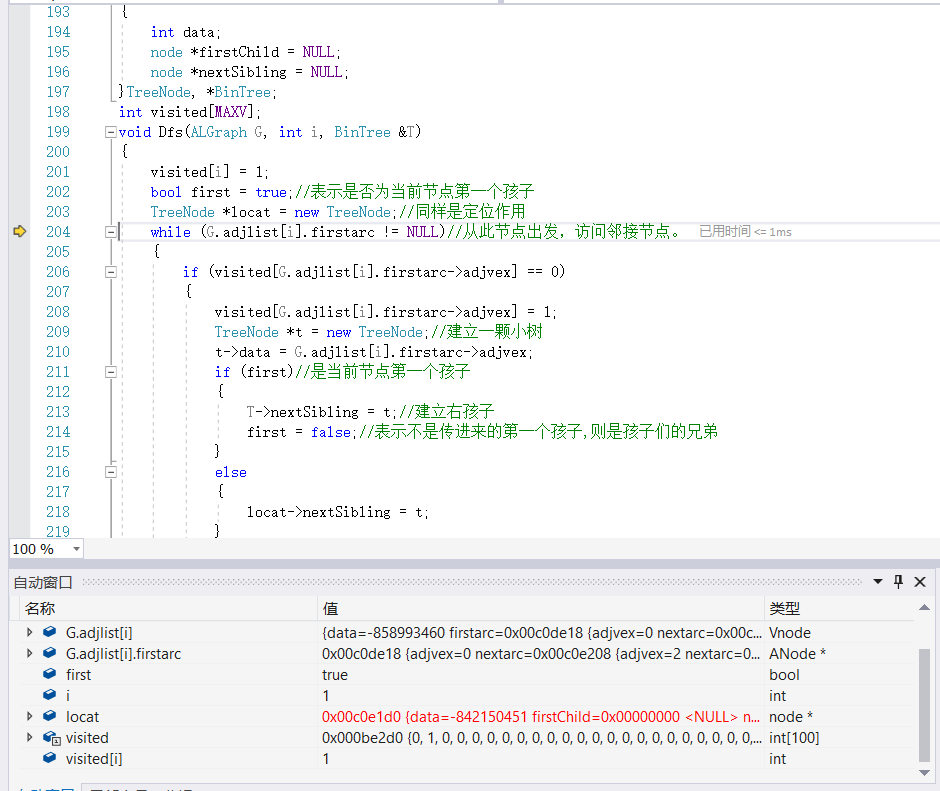
这时候按“继续”继续运行,到第二次循环时异常就出现了,请教大佬我应该如何修改这个程序,谢谢
