Problem Description
You have a sequence of numbers from which you must create the longest subsequence satisfying the following condition: it can be 'cut' into two parts that share exactly one common element (the last element of the first part is the first element of the second part), and the first part is sorted in strictly ascending order while the second part is sorted in strictly descending order. For example, the sequence { 1, 4, 6, 5, 2, 1 } can be 'cut' into { 1, 4, 6 } and { 6, 5, 2, 1 }. The two parts share the 6(see the following graph), and the first sequence is sorted in ascending order while the second sequence is sorted in descending order.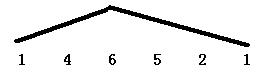
You are given a sequence of numbers. Output the minimal number of elements you must throw out from the given sequence such that the remaining subsequence satisfies the condition described above.
Input
There are multiple test cases. At first line of each case, there's an integer N (1<=N<=50) and N integers followed at second line representing the subsequence, each of which ranges from 1 to 1000000000.Input ends when N is 0.
Output
Output the result for each case in one line.
Sample Input
6
1 4 6 5 2 1
5
2 2 2 2 2
0
Sample Output
0
4
