这个程序插入的时候会出现问题。问了学校的老师，他就非让我跟书上写的一样。。。。我在这里给出示例的输入。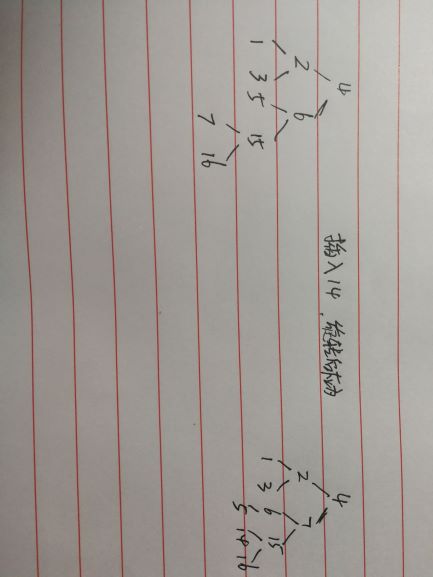
。希望大佬们能帮助一哈，困扰我蛮久了。。
输入的时候先序输入，比如图中的程序就应该输入：4 3,2 1,1 0,0 -1，0 -1,3 0，0 -1,0 -1,6 2,5 0,0 -1，0 -1,15 1,7 0,0 -1,0 -1,16 0,0 -1,0 -1（注：这里的叶子节点高度看做0，可以看成从叶子节点往上看的高度，第一个输入的值为节点的值，第二个输入的值为节点的高度）
我所给出的这个示例程序的含义就是先先序创建一个已经平衡的二叉树之后插入一个新的节点导致不平衡，然后进行旋转。
#include <stdio.h>
#include <stdlib.h>
typedef struct node
{
int data;
struct node *left;
struct node *right;
int height; //定义平衡二叉树的数据结构
}tree,*PTree;
int get_height(PTree T)
{
if(T==NULL)
return -1; //如果没有节点则为高度返回-1
else
return T->height; //否则返回当前节点的高度
}
void creat_tree(PTree &T) //先序创建平衡二叉树
{
int a;
printf("请输入元素:");
scanf("%d",&a);
/*printf("请输入高度:");
scanf("%d",&b);*/
if(a==0)
T=NULL;
else
{
T=(PTree)malloc(sizeof(tree));
T->data=a;
//T->height=b;
printf("请输入高度:");
scanf("%d",&T->height);
printf("创建左子树:\n");
creat_tree(T->left);
printf("请输入高度:");
scanf("%d",&T->height);
printf("创建右子树:\n");
creat_tree(T->right);
}
}
int Max(int a,int b) //用来得到高度的最大值，更新节点的高度
{
int max;
max=a;
if(b>a)
max=b;
return max;
}
PTree Single_L(PTree &T) //执行左侧单旋转例程
{
PTree p;
p=T;
T=T->left;
p->left=T->right;
T->right=p;
p->height=Max(get_height(p->left),get_height(p->right))+1;
T->height=Max(get_height(T->left),get_height(T->right))+1;
return T;
}
PTree Single_R(PTree &T) //执行右侧单旋转例程
{
PTree p;
p=T;
T=T->right;
p->right=T->left; //t的左右都比p的值要大，但是左子树的值要相比于右子树要更小，所以应该T的左子树等于p的右子树，左侧的单旋转同理
T->left=p;
p->height=Max(get_height(p->left),get_height(p->right))+1;
T->height=Max(get_height(T->left),get_height(T->right))+1;
return T;
}
PTree Double_L(PTree &T) //执行左侧双旋转例程（由2个单旋转例程构成）
{
T->left=Single_R(T->left);
return Single_L(T);
}
PTree Double_R(PTree &T) //执行右侧双旋转例程
{
T->right=Single_L(T->right);
return Single_R(T);
}
PTree insert(PTree &T,int x)
{
if(T==NULL) //如果找到了待插入的位置，就创建节点，将其高度设置为0
{
T=(PTree)malloc(sizeof(tree));
T->data=x;
T->height=0; //
T->left=T->right=NULL;
}
else
{
if(x<T->data)
{
T->left=insert(T->left,x);
if(get_height(T->left)-get_height(T->right)==2) //如果左子树的高度比右子树大2就不符合平衡二叉树的性质，需要执行旋转
{
if(x<T->left->data) //如果插入的元素和当前节点的值在同一侧，那么就执行单旋转
T=Single_L(T);
else
T=Double_L(T); //否则执行双旋转
}
}
else
{
if(x>T->data)
{
T->right=insert(T->right,x);
if(get_height(T->right)-get_height(T->left)==2) //如果右子树的高度比左子树大2就不符合平衡二叉树的性质，需要执行旋转
{
if(x>T->right->data)
T=Single_R(T); //如果插入的元素和当前节点的值在同一侧，那么就执行单旋转
else
T=Double_R(T); //否则执行双旋转
}
}
}
}
T->height=Max(get_height(T->left),get_height(T->right))+1; //更新节点的高度
return T;
}
void xianxubianli(PTree T)
{
if(T!=NULL)
{
printf("%d ",T->data);
//printf("%d ",T->height);
xianxubianli(T->left);
xianxubianli(T->right);
}
}
void main()
{
int a;
PTree T;
creat_tree(T);
xianxubianli(T);
printf("\n");
printf("please input the number you want to insert:");
scanf("%d",&a);
T=insert(T,a);
xianxubianli(T);
}
