谁会这个 望大家请教 拜托

Question

 

Answer 1

因为这里回答你没法直接插入公式，只能用图片跟你讲了。

第一题

表示函数 f(x) 与频谱 X(f) 之间关系的逆傅里叶变换公式是：

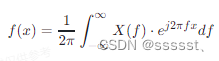
其中：

• f(x)是时域信号
• X(f)是频域信号，也就是f(x)的傅里叶变换
• e^j2πfx是复指数函数，其中j是虚数单位，满足j^2=-1
• df是积分中的微分元
• 积分的范围就是负无穷大到正无穷大，涵盖所有频率

第二题

信号x(t)的频谱为X(f)，根据傅里叶变换的时移性质，信号x(t-t0)的频谱X'(f)可以通过在院士频谱X(f)上乘一个相位因子来得到。这个相位因子是一个复指数函数，表示为e^-j2πft0，其中j是虚数单位，t0是时移量。
因此，信号x(t-t0)的频谱X'(f)为：

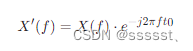
这个公式说明，时域中的时移对应于频域中的相位变化。如果 t0 是正数，则在频谱中会看到一个向左的相位旋转（对应于时域信号向右移动）；如果 t0 是负数，则会看到向右的相位旋转（对应于时域信号向左移动）。

第三题

如果信号 x(t) 的频谱为 X(f) ，那么频谱 X(f) 对应的信号是原始信号 x(t) 本身。在傅里叶变换中，时域信号 x(t) 和其频谱 X(f) 是互为变换对的关系。傅里叶变换将时域信号转换为频域信号，而傅里叶逆变换将频域信号转换回时域信号。

具体来说，X(f)是x(t)的傅里叶变换，表示为：

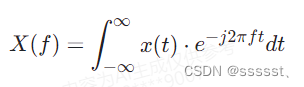
而x(t)是X(f)的傅里叶逆变换，表示为：

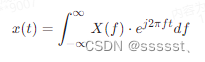
这里的e^j2πft和e^-j2πft分别是傅里叶变换和逆变换中的复指数核函数，其中j是虚数单位，f是频率变量，t是时间变量。

第四题

奈奎斯特定理指出，如果一个信号包含的最高频率成分是fmax，那么为了能够无失真地重建这个信号，采样频率fs必须至少是信号最高频率的两倍，即：

第五题

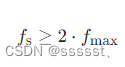
对于离散信号x(nΔ)，其频谱XΔ(f)通常是通过离散时间傅里叶变换来定义的。

如果我们用Δ表示采样间隔，那么采样频率fs就是其倒数，即

离散信号x(n)的离散时间傅里叶变换XΔ(f)定义为：

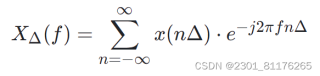
其中：

• XΔ(f)是离散信号x(nΔ)的频谱
• x(nΔ)是以采样间隔Δ采样的离散时间信号。
• e^j2πfnΔ是复指数函数，其中j是虚数单位，满足j^2=-1，f是频率变量
• 积分范围是从负无穷大到正无穷大，涵盖所有离散时间点。

在这个表达式中，n是整数，表示离散时间点的索引。由于Δ是采样间隔，所以nΔ实际上是连续时间t在采样点的对应值。因此，XΔ(f)描述了离散信号在频域的连续分布。

第六题

当一个离散信号 x(nΔ) 经过重抽样，其采样间隔从 Δ 变为 Δ1=mΔ（m 是一个整数），其频谱 XΔ1(f) 与原始频谱 XΔ(f) 之间的关系可以简化为：

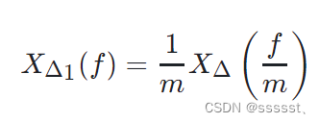
这意味着重抽样后的频谱是原始频谱的一个压缩版本，频率轴上的点被压缩了 m 倍。这种压缩是由于采样频率的改变引起的，采样频率从 Δ 分之一变为：

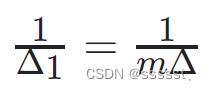
​这个关系只在满足奈奎斯特定理的情况下成立，即原始信号的带宽必须小于 2Δ 分之一以避免混叠现象。

第七题

根据傅里叶变换的性质，原始信号 x(t) 的频谱 X(f) 与用来滤波的频谱 H(f) 所对应的时间函数 h(t) 之间的关系是，滤波后的频谱 Y(f) 可以通过原始频谱 X(f) 与滤波频谱 H(f) 的乘积来得到：

第八题

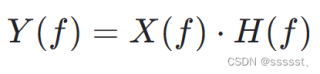
对于离散信号 x[n] 和其对应的频谱 X(k)，以及滤波器 h[n] 和其对应的频谱 H(k)，离散信号的频率域滤波公式可以表示为：

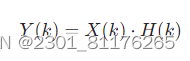
这里的 Y(k) 是滤波后的频谱。

然而，由于直接在频率域进行乘法可能会导致频谱混叠，通常会使用频率域的卷积定理，它指出离散时间信号的DFT与其时域卷积对应：

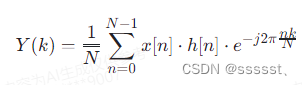
这里的 e^−j2πnk/N是由于直接在频率域乘法而引入的相位因子。

为了从滤波后的DFT Y(k) 重构时域信号 y[n]，我们使用DFT的逆变换，即逆离散傅里叶变换（IDFT）：

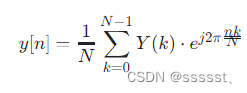
这样，我们就可以得到滤波后的时域信号 y[n]。

第九题

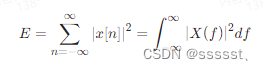
这里：

• E 是信号 x[n] 的能量。
• ∣x[n]∣ 是信号 x[n] 的绝对值。
• X(f) 是信号 x[n] 的傅里叶变换。
• ∣X(f)∣ 是频谱 X(f) 的绝对值。
• df 是积分中的微分元。

第十题

离散信号 y[n] 的 Z 变换表示为 Y(Z)，那么 y[−n] 的 Z 变换可以通过 Z 变换的位移性质来求得。

Z 变换的位移性质指出，如果将一个序列向后移动 k 个单位，那么其 Z 变换将会乘以 Z −k。对于 y[−n] 来说，它相当于将 y[n] 向后移动了 n 个单位，因此在 Z 域中，y[−n] 的 Z 变换 Y −n(Z) 将会是 Y(Z) 乘以 Z−n ：

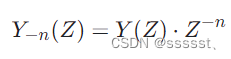
这里 Y −n(Z) 表示 y[−n] 的 Z 变换。

---

希望能帮助到你，谢谢。