数据分析的编程问题，4阶chebyshev级数、最佳平方逼近

Question

求函数 y=cosx 及函数y=cosh x 在区间[-1,1] 的4阶chebyshev级数以及4次多项式最佳平方逼近, 其中积分近似计算可以使用matlab命令quad及相关命令

Answer 1

你好，代码供参考
四阶切比雪夫

% 切比雪夫级数逼近
T0 = @(x) 1*ones(size(x));%切比雪夫多项式
T1 = @(x) x;
T2 = @(x) 2*x.^2 - 1;
T3 = @(x) 4*x.^3 - 3*x;
T4 = @(x) 8*x.^4 - 8*x.^2 + 1;
T = {T0, T1, T2, T3, T4};
A = zeros(5,5);
B1 = zeros(5,1);
B2 = zeros(5,1);
f1 = @(x)cos(x);
f2 = @(x)cosh(x);
for i = 1:1:5
    B1(i,1) = integral(@(x)T{i}(x).*f1(x), -1, 1);%积分获取右端项
    B2(i,1) = integral(@(x)T{i}(x).*f2(x), -1, 1);%积分获取右端项
    for j = 1:1:5
        A(i,j) = integral(@(x)T{i}(x).*T{j}(x), -1, 1);%积分获取系数矩阵
    end
end
c1 = A\B1;
c2 = A\B2;
y1 = @(x) c1(1)*T{1}(x) + c1(2)*T{2}(x) + c1(3)*T{3}(x) + c1(4)*T{4}(x) + c1(5)*T{5}(x);
y2 = @(x) c2(1)*T{1}(x) + c2(2)*T{2}(x) + c2(3)*T{3}(x) + c2(4)*T{4}(x) + c2(5)*T{5}(x);
x = linspace(-1,1,100);
ycos = cos(x);
ycosh = cosh(x);
ycos_fit = y1(x);
ycosh_fit = y2(x);
plot(x,ycos,'r-', x, ycosh, 'b-'); hold on;
plot(x,ycos_fit,'-.', x, ycosh_fit, 'g--');
legend('cos(x)','cosh(x)','cos(x)四阶切比雪夫逼近','cosh(x)四阶切比雪夫逼近')

效果

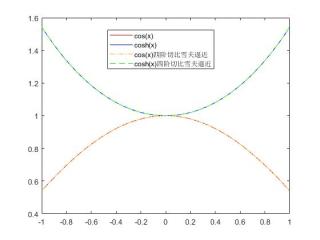
四次多项式逼近

% 四次多项式
T0 = @(x) 1*ones(size(x));%基函数
T1 = @(x) x;
T2 = @(x) x.^2;
T3 = @(x) x.^3;
T4 = @(x) x.^4;
T = {T0, T1, T2, T3, T4};
A = zeros(5,5);
B1 = zeros(5,1);
B2 = zeros(5,1);
f1 = @(x)cos(x);
f2 = @(x)cosh(x);
for i = 1:1:5
    B1(i,1) = integral(@(x)T{i}(x).*f1(x), -1, 1);%积分获取右端项
    B2(i,1) = integral(@(x)T{i}(x).*f2(x), -1, 1);%积分获取右端项
    for j = 1:1:5
        A(i,j) = integral(@(x)T{i}(x).*T{j}(x), -1, 1);%积分获取系数矩阵
    end
end
c1 = A\B1;
c2 = A\B2;
y1 = @(x) c1(1)*T{1}(x) + c1(2)*T{2}(x) + c1(3)*T{3}(x) + c1(4)*T{4}(x) + c1(5)*T{5}(x);
y2 = @(x) c2(1)*T{1}(x) + c2(2)*T{2}(x) + c2(3)*T{3}(x) + c2(4)*T{4}(x) + c2(5)*T{5}(x);
x = linspace(-1,1,100);
ycos = cos(x);
ycosh = cosh(x);
ycos_fit = y1(x);
ycosh_fit = y2(x);
plot(x,ycos,'r-', x, ycosh, 'b-'); hold on;
plot(x,ycos_fit,'-.', x, ycosh_fit, 'g--');
legend('cos(x)','cosh(x)','cos(x)四次多项式逼近','cosh(x)四次多项式逼近')

逼近效果：

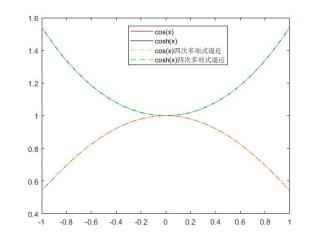
可见两者在四阶的时候，都和原函数十分贴合
有帮助还望答主点个右上角采纳支持一下，答题不易，十分感谢