用数组表示法（邻接矩阵）和邻接表两种存储结构分别表示下面的无向图。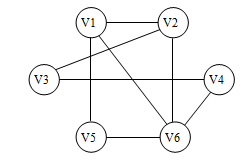

用数组表示法（邻接矩阵）和邻接表两种存储结构分别表示下面的无向图。图片说明

写回答
好问题 0 提建议
追加酬金
关注问题
分享
邀请回答
编辑收藏删除结题
收藏举报

1条回答默认最新

关注

码龄粉丝数原力等级 --

被采纳

被点赞

采纳率
MuShenSiMei 2019-04-11 17:48
关注
https://blog.csdn.net/curry___/article/details/81742727
这个链接是用临接矩阵和临接表表示无向图的具体例子简单易懂。

解决无用
评论打赏
分享
举报

评论

按下Enter换行，Ctrl+Enter发表内容

报告相同问题？

关注问题

如果表示某个图的邻接矩阵是不对称矩阵,则该图一定是有向图哈希算法散列表数据结构
2023-02-28 09:33

回答 2 已采纳 1，正确。因为如果是无向图，那么A节点可以通向B，B也可以通向A，那必然是偶数个1，即对称。而有向图规定这条边是A通向B，B无法通向A，即邻接矩阵中奇数个1，所以不对称。综上我觉得邻接矩阵不对称对应的
给一个图G的邻接矩阵，请你判断是否连通。用语言表示出来？
2017-11-26 01:06

回答 3 已采纳前面我回答了一个深度遍历的那个也是你的问题应该能够看到。遍历结束后若有node的标记为false则不联通
具有n个顶点的无向连通图采用邻接矩阵表示,则邻接矩阵中至少有数据结构算法
2023-03-14 14:09

回答 2 已采纳 1.你得先知道邻接矩阵是干什么用的它里面存的是n个顶点的连接关系既然题干里说了是连通图那么n个顶点就至少有n-1个连接每个连接由两个坐标来表示，这不就是2(n-1)个吗2.无权图，相邻顶点距离全部为1
图的三种存储结构：邻接矩阵表示法+链表法+十字链表法
2022-08-09 00:14

ོ栖落的博客图的三种存储结构：邻接矩阵表示法+链表法+十字链表法 C语言
C#语言中如何用邻接矩阵法表示图，并且遍历图？数据结构中图的遍历用C#的实现？数据结构
2015-12-17 15:07

回答 1 已采纳 http://download.csdn.net/download/yejinfu/2463153
c++邻接矩阵创建有向图，利用深度优先判断是否存在路径 c++ 数据结构深度优先
2022-12-28 21:22

回答 2 已采纳代码如下： #define _CRT_SECURE_NO_WARNINGS 1 #include <iostream> using namespace std; #define MVNUM
数据结构中有向图的邻接矩阵 数据结构算法
2023-02-27 11:07

回答 4 已采纳该回答引用GPTᴼᴾᴱᴺᴬᴵ一个有1000个顶点、1000条边的有向图的邻接矩阵有 1000 x 1000 = 1,000,000 个矩阵元素。判断这个邻接矩阵是否为稀疏矩阵需要看它的非零元素占据的
图的数组表示法c语言版,数据结构——图的数组（邻接矩阵）表示法
2021-05-22 18:53

月亮在营业的博客数组表示无向图用两个数组(vexs[],arcs[][])分别存储数据元素(顶点)的信息和数据元素之间的关系(边或弧)的信息。以二维数组表示有n个顶点的图时，需存放n个顶点信息和n^2个弧信息存储量。若考虑无向图的邻接矩阵的...
邻接表 给定一个具有n个点、m条边的有向图G，请输出其邻接表 c++ c语言
2022-05-15 19:51

回答 1 已采纳
请教数据结构#邻接链表表示图？ c语言
2019-06-20 17:41

回答 1 已采纳 printf("顶点表:%d",data[MAX].info); -> printf("顶点表:%d",data[i].info);
无向图的存储结构，求大神求大神
2014-11-13 07:33

回答 1 已采纳 01 #include 02 int main(void) 03 { int a[300][300]={0}; //初始化 04 int i,j,n,e,b; 05 sc
无向图的邻接矩阵（数组表示法）
2021-10-30 08:57

爱雨天的博客图的逻辑结构：多对多很难用多重链表表示 1.数组（邻接矩阵）表示法 ...一维数组Vexs[n]，叫顶点表，有n个，所以定义从0到n-1的数组，将n个顶点存储。...顶点之间哪两个有边，...来看无向图的例子：这个邻接矩阵...
C语言中临界矩阵转换为双向链域表示一个带权的无向图，设计一种算法的表示
2016-01-08 14:21

回答 1 已采纳相当于图的遍历，首先根据邻接矩阵构造节点，然后依次把边添加到图中。
有向图和无向图的表示方式(邻接矩阵，邻接表)
2023-09-08 06:15

dulu~dulu的博客有向图和无向图的表示方式(邻接矩阵，邻接表)：无向图，无向网，有向图，有向网的实现
图的两种存储：邻接矩阵和邻接表
2022-05-19 10:08

yyy_zxc的博客 无向图的边数组是对称矩阵 ==================*/ //---------------------定义邻接表类型 /*============= 图中顶点用一维数组或单链表存储【一般用数组存储】邻接列表的第i个列表是所有直接连接到第i个顶点的...
没有解决我的问题, 去提问

悬赏问题

¥15 关于#matlab#的问题：在模糊控制器中选出线路信息，在simulink中根据线路信息生成速度时间目标曲线（初速度为20m/s，15秒后减为0的速度时间图像）我想问线路信息是什么
¥15 banner广告展示设置多少时间不怎么会消耗用户价值
¥16 mybatis的代理对象无法通过@Autowired装填
¥15 可见光定位matlab仿真
¥15 arduino 四自由度机械臂
¥15 wordpress 产品图片 GIF 没法显示
¥15 求三国群英传pl国战时间的修改方法
¥15 matlab代码代写，需写出详细代码，代价私
¥15 ROS系统搭建请教（跨境电商用途）
¥15 AIC3204的示例代码有吗，想用AIC3204测量血氧，找不到相关的代码。

用数组表示法（邻接矩阵）和邻接表两种存储结构分别表示下面的无向图。

1条回答 默认 最新

悬赏问题

1条回答默认最新