普利姆算法问题，编译通过但是代码无输出

Question

题目描述
The island nation of Flatopia is perfectly flat. Unfortunately, Flatopia has no public highways. So the traffic is difficult in Flatopia. The Flatopian government is aware of this problem. They're planning to build some highways so that it will be possible to drive between any pair of towns without leaving the highway system.
Flatopian towns are numbered from 1 to N. Each highway connects exactly two towns. All highways follow straight lines. All highways can be used in both directions. Highways can freely cross each other, but a driver can only switch between highways at a town that is located at the end of both highways.
The Flatopian government wants to minimize the length of the longest highway to be built. However, they want to guarantee that every town is highway-reachable from every other town.

输入描述
This problem contains multiple test cases!
The first line of a multiple input is an integer T, then a blank line followed by T input blocks. Each input block is in the format indicated in the problem description. There is a blank line between input blocks.
For each case, the first line is an integer N (3 <= N <= 500), which is the number of villages. Then come N lines, the i-th of which contains N integers, and the j-th of these N integers is the distance (the distance should be an integer within [1, 65536]) between village i and village j.

输出描述
The output format consists of T output blocks. There is a blank line between output blocks.
For each case, you should output a line contains an integer, which is the length of the longest road to be built such that all the villages are connected, and this value is minimum.

我的代码为

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define N 110   //最多顶点数
#define MAX 0x3f3f3f3f  //模拟无穷大
int map[N][N];  //存储各顶点间的权值
int flag[N];    //标记是否已纳入树
int dis[N];     //已纳入点和其余各点的最小权值
int prim(int n)        //普利姆函数
{
    int i,j,l=0;
    int a[N]={0};
    int now;    //记录新纳入的点
    int min;    //记录新纳入的点到其余已纳入的点的最小权值
    memset(dis, MAX, sizeof(dis));  //初始化dis数组为无穷大
    memset(flag, 0, sizeof(flag));  //初始化flag数组，0表示此点未被纳入
    /*这里随机选取了1号点为初始时被纳入的顶点*/
    for(i = 1; i <= n; i++)
        dis[i] = map[1][i];     //与1号点与其他点的权值存入dis数组
    dis[1] = 0;         //一号点到其本身的权值为0
    flag[1] = 1;        //一号点标记为已纳入

    for(i = 1; i <=n; i++){         //除去初始时随机纳入的点还有n-1个点应被纳入
        now = min = MAX;            //初始为无穷大表示两点间无通路
        for(j = 1; j <= n; j++){    //遍历
            if(flag[j] == 0){
                if(dis[j] < min){   //寻找与已纳入各点权值最小的点
                    now = j;
                    min = dis[j];
                }
            }
        }
        a[++l]=min;
        if(now == MAX)      //若now等于max，则证明所有与初始时纳入的点连通的点已全被纳入
            break;
        flag[now] = 1;     //将找到的点纳入并标记
        for(j = 1; j <= n; j++){
            /*
                遍历比较之前纳入点到未纳入点的权值的最小值
                与刚纳入点到未纳入点的权值
                并用dis[j]存储新的最小值
            */
            if(flag[j] == 0){
                if(dis[j] > map[now][j]){
                    dis[j] = map[now][j];
                }
            }
        }
    }
    int r=0;
    for(int x=0;x<N;x++){
        if (a[x]>=r){
            r=a[x];
        }
    }
    return r;
}
int main()
{
    int i, j, k,T;
    scanf("%d",&T);
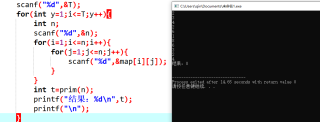
    for(int y=1;i<=T;y++){
        int n;
        scanf("%d",&n);
        for(i=1;i<=n;i++){
            for(j=1;j<=n;j++){
                scanf("%d",&map[i][j]);
            }
        }
        int t=prim(n);
        printf("%d\n",t);
        printf("\n");
    }
    
    return 0;
}

求解为何无输出！

Answer 1

你输入了吗