C# 用运算符重载创建定义复数相加、相减、相乘和相除的复数类Complex

Question

如何设计一个程序，使用运算符重载创建定义复数相加、相减、相乘和相除的复数类Complex，并根据用户输入实现复数类的加减乘除运算？

Answer 1

题主要的代码如下

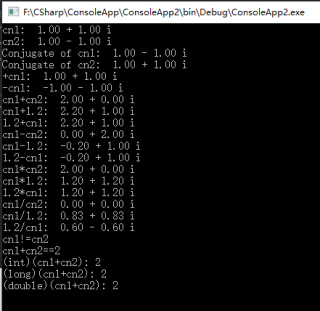
using System;
namespace ConsoleApp2
{/// <summary>
 /// 复数类
 /// </summary>
    class ComplexNumber
    {
        //实部
        double _RealPart;
        public double RealPart
        {
            get { return _RealPart; }
            set { _RealPart = value; }
        }

        //虚部
        double _ImaginaryPart;
        public double ImaginaryPart
        {
            get { return _ImaginaryPart; }
            set { _ImaginaryPart = value; }
        }

        /// <summary>
        /// 创建一个复数类实例
        /// </summary>
        /// <param name="rp">实部</param>
        /// <param name="ip">虚部</param>
        public ComplexNumber(double rp, double ip)
        {
            RealPart = rp;
            ImaginaryPart = ip;
        }

        /// <summary>
        /// 返回一个复数的共轭复数
        /// </summary>
        /// <param name="cn"></param>
        /// <returns></returns>
        public static ComplexNumber ConjugateOf(ComplexNumber cn)
        {
            return new ComplexNumber(cn.RealPart, -cn.ImaginaryPart);
        }

        /// <summary>
        /// 以字符串形式输出复数
        /// </summary>
        /// <returns></returns>
        public override string ToString()
        {
            //输出：实部 +/- 虚部 i 虚部前的加减号取决于虚部的正负
            return string.Format(" {0} {1} {2} i ",
                RealPart.ToString("#0.00"),
                ImaginaryPart >= 0 ? "+" : "-",
                Math.Abs(ImaginaryPart).ToString("#0.00"));
        }

        #region 重载一元运算符

        //取正、取负
        public static ComplexNumber operator +(ComplexNumber cn)
        { return cn; }
        public static ComplexNumber operator -(ComplexNumber cn)
        { return new ComplexNumber(-cn.RealPart, -cn.ImaginaryPart); }

        #endregion
        #region 重载二元运算符

        //加法 (a+bi)+(c+di)=(a+c)+(b+d)i
        public static ComplexNumber operator +(double num, ComplexNumber cn)
        { return new ComplexNumber(cn.RealPart + num, cn.ImaginaryPart); }
        public static ComplexNumber operator +(ComplexNumber cn, double num)
        { return new ComplexNumber(cn.RealPart + num, cn.ImaginaryPart); }
        public static ComplexNumber operator +(ComplexNumber cn1, ComplexNumber cn2)
        {
            return new ComplexNumber(
                cn1.RealPart + cn2.RealPart,
                cn1.ImaginaryPart + cn2.ImaginaryPart);
        }

        //减法 (a-bi)+(c-di)=(a-c)+(b-d)i
        public static ComplexNumber operator -(double num, ComplexNumber cn)
        { return new ComplexNumber(cn.RealPart - num, cn.ImaginaryPart); }
        public static ComplexNumber operator -(ComplexNumber cn, double num)
        { return new ComplexNumber(cn.RealPart - num, cn.ImaginaryPart); }
        public static ComplexNumber operator -(ComplexNumber cn1, ComplexNumber cn2)
        {
            return new ComplexNumber(
                cn1.RealPart - cn2.RealPart,
                cn1.ImaginaryPart - cn2.ImaginaryPart);
        }

        //乘法 (a+bi)*(c+di)=(ac-bd)+(ad+bc)i
        public static ComplexNumber operator *(double num, ComplexNumber cn)
        { return new ComplexNumber(cn.RealPart * num, cn.ImaginaryPart * num); }
        public static ComplexNumber operator *(ComplexNumber cn, double num)
        { return new ComplexNumber(cn.RealPart * num, cn.ImaginaryPart * num); }
        public static ComplexNumber operator *(ComplexNumber cn1, ComplexNumber cn2)
        {
            return new ComplexNumber(
                cn1.RealPart * cn2.RealPart - cn1.ImaginaryPart * cn2.ImaginaryPart,
                cn1.RealPart * cn2.ImaginaryPart + cn1.ImaginaryPart * cn2.RealPart);
        }

        //除法：
        //实数除以复数：n/(c+di)=n*(c-di)/(c*c+d*d)
        public static ComplexNumber operator /(double num, ComplexNumber cn)
        {
            return num * new ComplexNumber(cn.RealPart, -cn.ImaginaryPart) /
                (cn.RealPart * cn.RealPart + cn.ImaginaryPart * cn.ImaginaryPart);
        }
        //复数除以实数：(a+bi)/n=a/n+b/n*i
        public static ComplexNumber operator /(ComplexNumber cn, double num)
        {
            return new ComplexNumber(cn.RealPart / num, cn.ImaginaryPart / num);
        }
        //复数除以复数：(a+bi)/(c+di)=((ac+bd)+(ad+bc)i)/(c*c+d*d)
        public static ComplexNumber operator /(ComplexNumber cn1, ComplexNumber cn2)
        {
            double a = cn1.RealPart, b = cn1.ImaginaryPart;
            double c = cn2.RealPart, d = cn2.ImaginaryPart;
            return new ComplexNumber(a * c + b * d, a * d + b * c) / (c * c + d * d);
        }

        #endregion
        #region 重载关系运算符

        //等于
        public static bool operator ==(ComplexNumber cn1, ComplexNumber cn2)
        {
            return cn1.RealPart == cn2.RealPart &&
                cn1.ImaginaryPart == cn2.ImaginaryPart
                ? true : false;
        }
        public static bool operator ==(ComplexNumber cn, double n)
        { return cn.RealPart == n && cn.ImaginaryPart == 0 ? true : false; }
        public static bool operator ==(double n, ComplexNumber cn)
        { return cn.RealPart == n && cn.ImaginaryPart == 0 ? true : false; }

        //不等于
        public static bool operator !=(ComplexNumber cn1, ComplexNumber cn2)
        {
            return cn1.RealPart != cn2.RealPart ||
                cn1.ImaginaryPart != cn2.ImaginaryPart
                ? true : false;
        }
        public static bool operator !=(ComplexNumber cn, double n)
        { return cn.RealPart != n || cn.ImaginaryPart != 0 ? true : false; }
        public static bool operator !=(double n, ComplexNumber cn)
        { return cn.RealPart != n || cn.ImaginaryPart != 0 ? true : false; }

        //重载==和!=运算符后应该重写Equal是和GetHashCode函数
        //重写Equals函数
        public override bool Equals(object obj)
        {
            if (!(obj is ComplexNumber)) return false;
            else
            {
                ComplexNumber cn = (ComplexNumber)obj;
                if (this.RealPart != cn.RealPart) return false;
                if (this.ImaginaryPart != cn.ImaginaryPart) return false;
                return true;
            }
        }
        //重写GetHashCode函数
        public override int GetHashCode()
        { return base.GetHashCode(); }

        #endregion
        #region 重载true和false

        //实部和虚部至少有一个不为0时，为true，否则为false
        public static bool operator true(ComplexNumber cn)
        { return cn.RealPart != 0 || cn.ImaginaryPart != 0 ? true : false; }
        public static bool operator false(ComplexNumber cn)
        { return cn.RealPart == 0 && cn.ImaginaryPart == 0 ? true : false; }

        #endregion
        #region 转换运算符

        //只能显示转换，强制转换时舍弃虚部
        public static explicit operator int(ComplexNumber cn) { return (int)cn.RealPart; }
        public static explicit operator long(ComplexNumber cn) { return (long)cn.RealPart; }
        public static explicit operator double(ComplexNumber cn) { return cn.RealPart; }

        #endregion
    }
    class Program
    {
        static void Main(string[] args)
        {
            ComplexNumber cn = new ComplexNumber(1, 1);

            //两个复数
            ComplexNumber cn1 = new ComplexNumber(1, 1);
            ComplexNumber cn2 = new ComplexNumber(1, -1);

            //打印复数
            Console.WriteLine("cn1: " + cn1);
            Console.WriteLine("cn2: " + cn2);

            //求复数的共轭复数
            Console.WriteLine("Conjugate of cn1: " + ComplexNumber.ConjugateOf(cn1));
            Console.WriteLine("Conjugate of cn2: " + ComplexNumber.ConjugateOf(cn2));

            //复数取正负
            Console.WriteLine("+cn1: " + (+cn1));
            Console.WriteLine("-cn1: " + (-cn1));

            //复数加法
            Console.WriteLine("cn1+cn2: " + (cn1 + cn2));
            Console.WriteLine("cn1+1.2: " + (cn1 + 1.2));
            Console.WriteLine("1.2+cn1: " + (1.2 + cn1));

            //复数减法
            Console.WriteLine("cn1-cn2: " + (cn1 - cn2));
            Console.WriteLine("cn1-1.2: " + (cn1 - 1.2));
            Console.WriteLine("1.2-cn1: " + (1.2 - cn1));

            //复数乘法
            Console.WriteLine("cn1*cn2: " + (cn1 * cn2));
            Console.WriteLine("cn1*1.2: " + (cn1 * 1.2));
            Console.WriteLine("1.2*cn1: " + (1.2 * cn1));

            //复数除法
            Console.WriteLine("cn1/cn2: " + (cn1 / cn2));
            Console.WriteLine("cn1/1.2: " + (cn1 / 1.2));
            Console.WriteLine("1.2/cn1: " + (1.2 / cn1));

            //检验是否相等
            if (cn1 == cn2) { Console.WriteLine("cn1==cn2"); }
            if (cn1 != cn2) { Console.WriteLine("cn1!=cn2"); }
            if (cn1 + cn2 == 2) { Console.WriteLine("cn1+cn2==2"); }
            if (cn1 + cn2 != 2) { Console.WriteLine("cn1+cn2!=2"); }

            //显式类型转换
            Console.WriteLine("(int)(cn1+cn2): " + (int)(cn1 + cn2));
            Console.WriteLine("(long)(cn1+cn2): " + (long)(cn1 + cn2));
            Console.WriteLine("(double)(cn1+cn2): " + (double)(cn1 + cn2));

            Console.ReadLine();
        }
    }
}

有其他问题可以继续交流~