各位请问为什么在“ 中点的f值很小但不一定是根”的这种情况时会运行超时呢

Question

题目
二分法求函数根的原理为：如果连续函数f(x)在区间[a,b]的两个端点取值异号，即f(a)f(b)<0，则它在这个区间内至少存在1个根r，即f(r)=0。

二分法的步骤为：

检查区间长度，如果小于给定阈值，则停止，输出区间中点(a+b)/2；否则
如果f(a)f(b)<0，则计算中点的值f((a+b)/2)；
如果f((a+b)/2)正好为0，则(a+b)/2就是要求的根；否则
如果f((a+b)/2)与f(a)同号，则说明根在区间[(a+b)/2,b]，令a=(a+b)/2，重复循环；
如果f((a+b)/2)与f(b)同号，则说明根在区间[a,(a+b)/2]，令b=(a+b)/2，重复循环。

#include <stdio.h>
double a1,a2,a3,a4;
double f(double x){
    double y;
    y=a4*x*x*x + a3*x*x + a2*x + a1;
    return y;    
}
int main(){
    double a,b;
    double r,y;
    scanf("%lf %lf %lf %lf",&a4,&a3,&a2,&a1);
    scanf("%lf %lf",&a,&b);
    if((b-a)<0.01){
        r=(a+b)/2.0;
        printf("%.2f",r);
    }else{
        while(f(a)*f(b)<0){
            y=f((a+b)/2.0);
            if(y==0){
                r=(a+b)/2.0;
                printf("%.2f",r);
                break;
            }else if(y*f(a)>=0){
                a=(a+b)/2.0;
            }else if(y*f(b)>=0){
                b=(a+b)/2.0;
            }
        }
    }
}

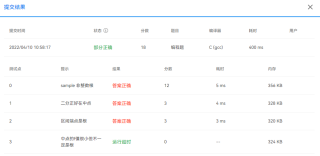
运行结果及报错内容

Answer 1

if(y==0) 这个最好是y小于一个很小数，不能直接与0进行相等判断，比如 if(y< 1e-6)
另外if((b-a)<0.01){是怎么考虑的，为什么是小于0.01呢，另外a>b或者b>a两种情况都是一样处理么