这里显示运行超时了，请问该怎么解决

Question

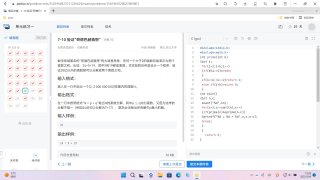
可以在枚举的基础上优化吗
还是说只能换算法，如果是，应该怎么操作？

Answer 1

写个C#你自己看（啥语言无所谓，意思都是一个意思，能看懂就可以自己改）

int n = 2_000_000_000;
//int n = 4;

//题目特殊，可以优化
//n是偶数，那么除了 2+2这个特殊玩意，任何偶数都可以拆成 奇数+奇数，所有后续我们用奇数判定
//在n是偶数情况下，2x+2y 除了x，y为1的情况，其他情况绝对不会是2个素数
//而2+2=4有恰恰有1+3的解，而且符合题目要求的最小解
for (int i = 1; i < n/2; i=i+2)
{
    int j = n - i;
    if (isn(i, j))
    {
       // 请输出i，j
       break;
    }
}

bool isn(int a, int b)
{
    bool res = true;
    //因为进来的都是奇数，所以2无需判定,同时能被偶数整除的就一定能被2整除，就一定不是奇数（前面4的情况讨论过1+3就有结果，所以这里步长可以优化成2）
    for (int i = 3; i <Math.Sqrt(b); i=i+2)
    {
        if (i <= a&&a%i==0)
        {
            return false;
        }
        if (b%i==0)
        {
            return false;
        }
    }
    return res;
}