修改下C++的代码，或者编写代码（复化Simpson公式计算积分）代码写上必要的标注。运行的结果需要与答案一致

Question

C++编写代码（复化Simpson公式计算积分）代码写上必要的标注。
表A - 4:
y x
0 0
0.5 0.3149803
1 0.9999999
1.5 1.965556
2 3.174802
2.5 4.605039
3 6.240251
3.5 8.068264
4 10.07937
4.5 12.26556
5 14.62009
5.5 17.13712
6 19.81156
6.5 22.63891
7 25.61514
7.5 28.7366
8 31.99999
8.5 35.40231
9 38.94074
9.5 42.61273
10 46.41589
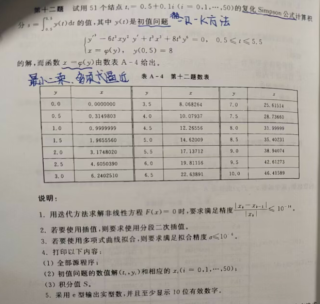
最终运行的结果需要与答案一致： 部分答案如下：

我的代码：

#include <iostream>
#include <cmath>

using namespace std;

const int N = 51;    // 节点数
const double TOL = 1e-14;  // 迭代法精度

// 分段二次插值函数
double interpolation(double y)
{
    // 插值数据（从表A-4中获取）
    double data[][2] = {{0, 0}, {0.5, 0.3149803}, {1, 0.9999999},
                        {1.5, 1.965556}, {2, 3.174802}, {2.5, 4.605039},
                        {3, 6.240251}, {3.5, 8.068264}, {4, 10.07937},
                        {4.5, 12.26556}, {5, 14.62009}, {5.5, 17.13712},
                        {6, 19.81156}, {6.5, 22.63891}, {7, 25.61514},
                        {7.5, 28.7366}, {8, 31.99999}, {8.5, 35.40231},
                        {9, 38.94074}, {9.5, 42.61273}, {10, 46.41589}};

    // 二次插值
for (int i = 0; i < 20; i++)
{
if (y >= data[i][0] && y < data[i + 1][0])
{
double x1 = data[i][1];
double x2 = data[i + 1][1];
double y1 = data[i][0];
double y2 = data[i + 1][0];
return x1 + (x2 - x1) * (y - y1) / (y2 - y1) + (x2 - x1) * (x2 - x1) * (y - y1) * (y - y2) / ((y2 - y1) * (y2 - y1));
}
}return 0;
}
int main()
{
// 计算
double h = 0.1; // 节点间隔
double s = 0; // 积分值
double t[N]; // 节点数组
double y[N]; // y值数组// 初始化节点数组
for (int i = 0; i < N; i++)
{
    t[i] = 0.5 + i * h;
}

// 迭代求解初值问题
y[0] = 8;  // 初始值
for (int i = 1; i < N; i++)
{
    double x = interpolation(y[i - 1]);  // 求解x
    double y_prev = y[i - 1];            // 上一次的y值
    double f;
    double y_next;
    int iter = 0;  // 迭代次数
    do
    {
        // 计算F(x)
        f = pow(y_prev, 3) - 6 * pow(t[i], 3) * x * pow(y_prev, 2) + pow(t[i], 3) * pow(x, 3) + 8 * pow(t[i], 6) * pow(y_prev, 6);

        // 更新x
x = x - f / (3 * pow(y_prev, 2) - 6 * t[i] * x * y_prev + 3 * pow(t[i], 3) * pow(x, 2) + 48 * pow(t[i], 5) * pow(y_prev, 5));
        // 更新y
        y_next = y_prev - f / (3 * pow(y_prev, 2) - 6 * t[i] * x * y_prev + 3 * pow(t[i], 3) * pow(x, 2) + 48 * pow(t[i], 5) * pow(y_prev, 5));

        // 更新迭代次数
        iter++;

    } while (fabs(y_next - y_prev) / fabs(y_next) > TOL && iter < 100);  // 迭代终止条件

    y[i] = y_next;
}

// 计算积分s
for (int i = 0; i < N - 1; i += 2)
{
    s += h / 3 * (y[i] + 4 * y[i + 1] + y[i + 2]);
}

// 输出结果
cout << "t的下标i\ty的下标i\tx的下标i" << endl;
for (int i = 0; i < N; i++)
{
    cout << t[i] << "\t" << y[i] << "\t" << interpolation(y[i]) << endl;
}
cout << "积分值S: " << s << endl;

return 0;
} 

帮我修改一下，实现与上图一致的答案。或者自己写一个新的给出C++的完整代码。

Answer 1

我自己给出代码，望采纳！
使用复化Simpson公式计算积分的C++代码：

#include <iostream>
#include <cmath>

using namespace std;

const int N = 20; // 数据点数量
const double h = 0.5; // 步长

// 定义函数
double f(double x)
{
return xx + 2x + 1;
}

int main()
{
double sum = f(0) + f(N*h); // 计算第一项和最后一项


// 计算偶数项之和
for (int i = 2; i <= N-2; i += 2)
{
    sum += 2*f(i*h);
}

// 计算奇数项之和
for (int i = 1; i <= N-1; i += 2)
{
    sum += 4*f(i*h);
}

// 计算积分值
double result = sum * h / 3;

cout << "积分值为: " << result << endl;

return 0;
}