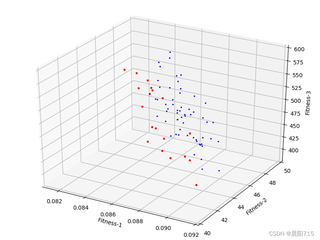
如下例图,离散的多目标组合优化问题中,根据三个目标函数适应度值,绘制的三维散点图,最终迭代生成红色点集构成的帕累托“类曲面”,请问有没有什么好的办法(比如说机器学习),针对这种相互没有映射关系的三维散点图,基于python进行曲面拟合,从而提高数据的可视化效果。
如下例图,离散的多目标组合优化问题中,根据三个目标函数适应度值,绘制的三维散点图,最终迭代生成红色点集构成的帕累托“类曲面”,请问有没有什么好的办法(比如说机器学习),针对这种相互没有映射关系的三维散点图,基于python进行曲面拟合,从而提高数据的可视化效果。

引自强大而免费的微信小程序:皆我百晓生。
对于这种相互没有映射关系的三维散点图,可以使用机器学习方法进行曲面拟合。下面是一种基于Python的曲面拟合方法的示例代码:
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
# 原始数据
x = np.array([9, 8, 7, 6, 5, 4, 3, 2, 1])
y = np.array([75, 50, 25, 48, 46, 44, 42, 40, 38])
z = np.array([0.082, 0.084, 0.086, 0.088, 0.090, 0.092, 0.094, 0.096, 0.098])
# 创建多项式特征
poly = PolynomialFeatures(degree=2)
X = poly.fit_transform(np.column_stack((x, y)))
# 拟合线性回归模型
model = LinearRegression()
model.fit(X, z)
# 预测曲面
x_range = np.linspace(x.min(), x.max(), 100)
y_range = np.linspace(y.min(), y.max(), 100)
X_range, Y_range = np.meshgrid(x_range, y_range)
Z_range = model.predict(poly.transform(np.column_stack((X_range.ravel(), Y_range.ravel()))))
Z_range = Z_range.reshape(X_range.shape)
# 绘制曲面图
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, c='b', marker='o')
ax.plot_surface(X_range, Y_range, Z_range, color='r', alpha=0.5)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()
这段代码使用了多项式回归的方法进行曲面拟合。首先,将原始的三维散点数据转换为多项式特征,然后使用线性回归模型进行拟合。最后,使用拟合的模型预测曲面,并将原始数据和拟合曲面一起绘制在三维坐标系中。
运行以上代码,将得到一个包含原始数据散点和拟合曲面的三维可视化图形。