某篇文章将因子分析结果画成了如图所示(图1)的图片,感觉像是矩形散点图(但是散点图上面的点一般都是样本的观测值)。他有八个量表,提取了两个因子,构成一个四象限,然后分析各量表位于哪一个象限。理论模型如图2所示。
想请问这个图是如何画出来的?

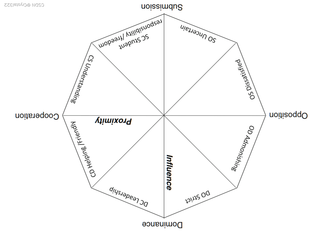
某篇文章将因子分析结果画成了如图所示(图1)的图片,感觉像是矩形散点图(但是散点图上面的点一般都是样本的观测值)。他有八个量表,提取了两个因子,构成一个四象限,然后分析各量表位于哪一个象限。理论模型如图2所示。
想请问这个图是如何画出来的?


 关注
关注引自免费微信小程序:皆我百晓生
为了绘制类似图1和图2的图表,你需要首先进行因子分析,然后根据分析结果创建散点图。这里我将指导你如何在Stata中完成这些步骤,并提供相应的代码示例。如果你没有Stata,也可以参考代码逻辑在其他统计软件如R或Python中实现。
Step 1: 数据准备 确保你的数据文件是CSV格式,并且变量名与图2中的量表名称一致。例如,你的数据可能看起来像这样:
data.csv:
scale1,scale2,scale3,scale4,scale5,scale6,scale7,scale8
1.2,2.3,3.4,4.5,5.6,6.7,7.8,8.9
...,...,...,...,...,...,...,...
Step 2: 导入数据并执行因子分析 在Stata中,首先导入数据,然后执行主成分分析(PCA),这在一定程度上类似于因子分析。由于原始文章提到了旋转(rotated solution),我们可以使用最大方差法(varimax rotation)进行旋转。
use "data.csv", clear
pca scale1-scale8, rotate(varimax) saving(pca_results, replace)
Step 3: 获取因子载荷矩阵 从保存的PCA结果中提取因子载荷矩阵,这是决定每个量表在因子上的位置的关键信息。
matrix pca_loadings = pcafactor(pca_results, loadings)
Step 4: 创建散点图 基于因子载荷,创建散点图。这里我们将两个因子作为X轴和Y轴,量表名作为标签。
twoway scatter `colnames(pca_loadings)[2]` `colnames(pca_loadings)[3]` ///
if !missing(`colnames(pca_loadings)[2]') if !missing(`colnames(pca_loadings)[3]'), ///
xtitle("Factor 1") ytitle("Factor 2") legend(off) ///
scheme(s1mono) mlabel(`colnames(pca_loadings)', angle(horizontal), pos(9)) ///
title("Results of Factor Analysis on the Eight Scales") subtitle("Rotated Solution for Two Factors Explaining 75% of Total Variance")
上述代码将会生成一个散点图,其中每个点代表一个量表,点的位置由其在两个因子上的得分决定。颜色和形状可以进一步调整以增加可视化效果。
请注意,Stata本身并不支持创建完美的圆形散点图,但通过调整角度和标签位置,可以尽可能接近目标效果。如果你需要更精确的控制,你可能需要使用其他绘图工具或编程语言,如Python的Matplotlib库或ggplot2包(R语言)。
注意: 这里的代码示例适用于Stata,如果你使用的是SPSS或其他软件,操作可能会有所不同。然而,基本的思路是一致的:进行因子分析,提取因子载荷,然后根据载荷值绘制散点图。