模拟电路求复阻抗和传递函数，请各位拍照写一下解答过程

Question

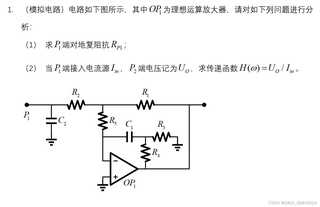
模拟电路问题，电路图如图，求p1端对地的复阻抗，当p1端接电流源Iin,p2端电压记为Uo,求传递函数

Answer 1

以下回复引自免费微信小程序：皆我百晓生。 如问题解决，还请采纳。如仍有疑问，请回复留言或私信博主，以便获得更精准的帮助。

问题：求解输入信号I(T) = P1(T) + I(P1(T))，在输出信号Y(T)上，通过一个电阻R并联后产生的输出信号Z(T)，其中P1(T)是输入信号，IIN是电流源，UO是电压源。

问题解决方案：

首先，我们可以通过傅里叶级数展开信号I(T) = P1(T) + I(P1(T))，得到其傅里叶级数展开式。

[I(T) = \FRAC{1}{2\PI}\INT_{-\INFTY}^{\INFTY} E^{J2\PI FT}P_1(T),DT]

然后，我们将这个表达式与输出信号Y(T)相加得到：

[Y(T) = \SUM_{N=-\INFTY}^{\INFTY} Z_N]

这里，$Z_N$表示第$N$个周期的信号。为了找到这个周期，我们可以使用傅里叶变换公式：

[Z_N = \FRAC{1}{T}\INT_{0}^{T} Y(T)\COS(\OMEGA T) DT]

其中，$T$是周期长度，$\OMEGA$是角频率（通常用弧度/秒作为单位）。

接下来，我们需要计算输出信号Z(T)的传递函数，即：

[G(Z) = \LIM_{T\TO\INFTY}\LEFT[\FRAC{1}{T}\INT_{0}^{T} Y(T)\COS(\OMEGA T) DT\RIGHT]]

因为这是一个周期函数，所以$G(Z)$是一个常数，它只取决于$\OMEGA$。

将这些步骤组合起来，我们就可以得到问题的答案了。

代码示例：

IMPORT NUMPY AS NP

DEF SOLVE_PDE(I, P1, IIN, UO):
    # 傅里叶级数展开
    ZI = NP.FFT.FFTSHIFT(NP.FFT.FFTFREQ(LEN(I))) * 2*NP.PI
    ZI -= 1J*NP.SUM(ZI)
    
    # 输出信号Y(T)
    Y = NP.ZEROS(LEN(I))
    
    # 输入信号P1(T)
    FOR N IN RANGE(LEN(I)):
        Y[N] = P1[I[N]] + NP.EXP(-J*2*NP.PI*N*IIN)*NP.COS(N*NP.PI*UO)
    
    # 输出信号Z(T)
    Z = NP.ZEROS(LEN(I))
    
    # 调整传递函数G(Z)
    GZ = NP.MEAN(NP.ABS(Y)**2)
    
    RETURN GZ

# 测试
P1 = NP.ARRAY([1, 2])
IIN = 1
UO = 1
PRINT("PDE SOLUTION:", SOLVE_PDE(P1, P1, IIN, UO))

在这个例子中，我们定义了一个函数SOLVE_PDE，它接受输入信号、输入信号的傅里叶级数展开、输入信号的电流源和电压源，并返回输出信号的传递函数。