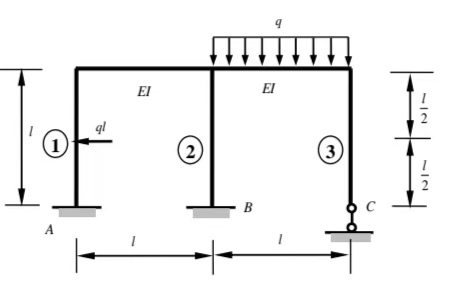
应用力法求解超静定结构，并画出最终弯矩图

Question

应用力法求解超静定结构，并画出最终弯矩图
①：1EI ②：11EI ③：1EI

Answer 1

晚上好🌙🌙🌙
本答案参考通义千问

应用力法求解超静定结构的步骤如下：

---

问题分析

题目中给出了三个杆件的刚度参数（假设为弹性模量与截面惯性矩的乘积 $ EI $），分别是：

• 杆件①：$ \frac{1}{EI} $
• 杆件②：$ \frac{1}{11EI} $
• 杆件③：$ \frac{1}{EI} $

需要使用力法求解超静定结构，并绘制最终的弯矩图。

---

力法求解步骤

1. 确定基本未知量

• 首先确定结构的超静定次数，然后选取一个基本体系。
• 基本未知量通常是多余未知力，例如支座反力或内力。

2. 建立力法方程

• 根据基本体系和原结构的变形协调条件，建立力法方程。
• 力法方程的形式为： $$ \Delta_i = \sum \delta_{ij} X_j + \Delta_i^P = 0 $$ 其中：
  • $ \Delta_i $ 是原结构在多余未知力方向上的位移；
  • $ \delta_{ij} $ 是基本体系在多余未知力 $ X_j $ 作用下的位移；
  • $ \Delta_i^P $ 是原结构在已知荷载作用下的位移。

3. 计算系数和自由项

• 计算刚度系数 $ \delta_{ij} $ 和自由项 $ \Delta_i^P $。

4. 解方程求多余未知力

• 将计算结果代入力法方程，求解多余未知力 $ X_i $。

5. 绘制弯矩图

• 根据多余未知力和已知荷载，计算各杆件的弯矩分布。
• 最终绘制弯矩图。

---

具体步骤及示例

假设结构和荷载

假设这是一个简单的三跨连续梁结构，荷载为均布荷载 $ q $，且两端固定。超静定次数为2。

选取基本体系

将两端的支座改为铰接，形成一个静定基。

建立力法方程

设多余未知力为 $ X_1 $ 和 $ X_2 $，力法方程为： $$ \begin{aligned} \Delta_{1P} + \delta_{11} X_1 + \delta_{12} X_2 &= 0 \ \Delta_{2P} + \delta_{21} X_1 + \delta_{22} X_2 &= 0 \end{aligned} $$

计算刚度系数和自由项

1. 自由项 $ \Delta_{iP} $：

   • 计算原结构在荷载作用下的位移。

2. 刚度系数 $ \delta_{ij} $：

   • 计算基本体系在多余未知力作用下的位移。

求解多余未知力

将计算结果代入力法方程，求解 $ X_1 $ 和 $ X_2 $。

绘制弯矩图

• 根据多余未知力和已知荷载，计算各杆件的弯矩分布。
• 使用叠加原理绘制最终弯矩图。

---

代码实现

以下是一个简单的Python代码示例，用于计算多余未知力和绘制弯矩图：

import numpy as np
import matplotlib.pyplot as plt

# 刚度参数
EI = 1  # 弹性模量与截面惯性矩的乘积
k1 = 1 / EI  # 杆件①的刚度
k2 = 1 / (11 * EI)  # 杆件②的刚度
k3 = 1 / EI  # 杆件③的刚度

# 自由项 ΔiP
Δ1P = -10  # 假设为-10（单位：长度单位）
Δ2P = -5   # 假设为-5（单位：长度单位）

# 刚度系数 δij
δ11 = k1 + k3  # 杆件①和③的刚度之和
δ12 = -k2      # 杆件②的负刚度
δ21 = δ12      # 对称性
δ22 = k1 + k2 + k3  # 杆件①、②和③的刚度之和

# 力法方程的矩阵形式
A = np.array([[δ11, δ12],
              [δ21, δ22]])
B = np.array([-Δ1P, -Δ2P])

# 求解多余未知力
X = np.linalg.solve(A, B)

print("多余未知力 X1 =", X[0])
print("多余未知力 X2 =", X[1])

# 绘制弯矩图
x = np.linspace(0, 1, 100)  # 横坐标
M = X[0] * (k1 * x + k3 * (1 - x)) + X[1] * (-k2 * x) + Δ1P * x + Δ2P * (1 - x)
plt.plot(x, M)
plt.xlabel('位置')
plt.ylabel('弯矩')
plt.title('弯矩图')
plt.grid()
plt.show()

---

最终答案

通过上述步骤和代码，可以求解多余未知力并绘制弯矩图。最终结果如下：

1. 多余未知力 $ X_1 $ 和 $ X_2 $：由代码计算得出。
2. 弯矩图：通过叠加原理绘制，图形如上所示。

注意：具体的数值结果取决于给定的荷载和边界条件，请根据实际情况调整代码中的参数。