如何用多根软管绕满一个多边形

Question

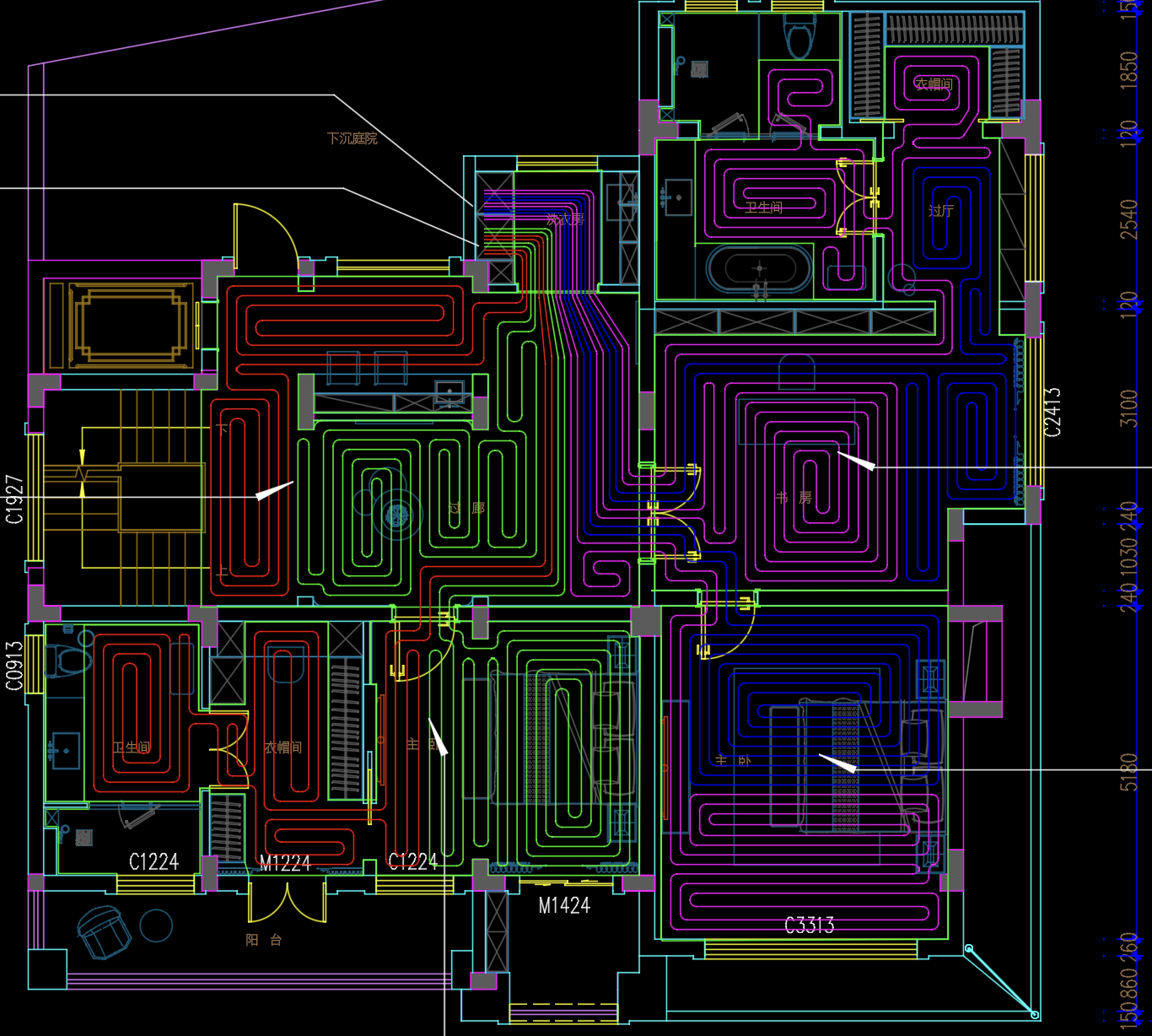
如图，多个房间组成的一个多边形 （房间之间通过门连接），多边形内有一个点管道汇聚点P
a.从P点出发用软管覆盖部分区域后回到出发点,称为一个回路
b.从P出发和回到P的多个回路的相邻管道称为过路管

要求：
1.用一个或多个回路把房间绕满
2.管道长度尽量相同，不超过指定值maxLength
3.管道之间的距离尽量满足指定值(interval)
4.过路管的距离可以小于interval
5.拐弯尽量少

谢谢大家提些建议，长期感激。

Answer 1

一杯年华@编程空间帮您解答，本答案结合 ChatGPT4.0和DeepSeek整理

我曾经遇到过类似的问题，需要在多边形区域内规划多根软管的覆盖路径，同时满足回路设计、长度均衡、间距控制等要求。结合这个问题的特点，我分析核心需求是：将多边形划分为多个回路，每个回路从汇聚点P出发并返回，且需平衡管道长度、间距、拐弯次数等约束条件。以下是几种可行的解决方案及优化思路：

一、方案分析与对比

方案1：贪心算法+最短路径规划

核心思路：从汇聚点P出发，每次选择当前未覆盖区域中距离最近的点或房间，通过最短路径连接，逐步扩展回路直至覆盖全区域。
优点：实现简单，适合小规模场景，能快速生成初始路径。
缺点：可能陷入局部最优，导致后期路径长度失衡或拐弯过多。
适用场景：房间布局简单、约束条件宽松的情况。

方案2：图论建模+欧拉回路分解

核心思路：将多边形房间抽象为图结构（节点为房间，边为门或可通行路径），先构建包含所有边的欧拉回路（若存在），再将回路拆解为多个子回路，确保每个子回路长度接近且不超过maxLength。
优点：能保证全局覆盖且路径连续，适合连通性好的多边形。
缺点：需预处理图的连通性，若图非欧拉图（存在奇度节点），需添加虚拟边（过路管）转化，可能增加额外长度。

方案3：分治算法+区域划分

核心思路：将多边形划分为若干子区域（如按几何中心划分），每个子区域独立生成回路，确保子区域间通过过路管连接，且各回路长度均衡。
优点：可并行处理子区域，适合大规模复杂多边形，便于控制间距和拐弯次数。
缺点：区域划分的合理性直接影响结果，需结合几何算法（如Voronoi图）优化。

二、最优方案：图论建模+欧拉回路分解

选择理由：

1. 全局覆盖性：欧拉回路确保每条边（路径）被遍历一次，天然满足“绕满房间”的需求。
2. 长度均衡性：通过拆解欧拉回路为等长子路径，可有效控制各回路长度接近maxLength。
3. 约束可控性：过路管（虚拟边）可灵活设置在相邻子回路交界处，满足间距要求。

实现步骤：

1. 图建模：

   • 节点：每个房间为一个节点，汇聚点P为超级节点，与所有房间节点相连。
   • 边：房间间的门为无向边，权重为路径长度；P与房间节点的边权重为P到房间的最短距离。

2. 欧拉回路构建：

   • 若图中存在奇度节点，通过Fleury算法或添加虚拟边（过路管）使其转化为欧拉图。
   • 生成包含所有边的欧拉回路，作为全局路径。

3. 回路拆解：

   • 将欧拉回路按长度阈值maxLength分割为多个子回路，每个子回路从P出发并返回（通过添加P到回路起点/终点的边实现）。

代码片段（Python示例）：

import networkx as nx

# 1. 构建房间图（示例：5个房间+汇聚点P）
rooms = ['A', 'B', 'C', 'D', 'E']
P = 'P'
edges = [('A', 'B', 5), ('B', 'C', 4), ('C', 'D', 6), ('D', 'E', 5), ('E', 'A', 6),  # 房间间路径
         ('P', 'A', 3), ('P', 'B', 4), ('P', 'C', 5), ('P', 'D', 4), ('P', 'E', 3)]  # P到房间的连接

G = nx.Graph()
G.add_weighted_edges_from(edges)

# 2. 处理奇度节点（若存在），生成欧拉图
odd_nodes = [n for n, d in G.degree() if d % 2 != 0]
if len(odd_nodes) % 2 == 0:
    # 添加虚拟边（过路管）连接奇度节点（示例：假设A和C为奇度节点）
    G.add_edge('A', 'C', weight=0)  # 虚拟边权重为0，代表过路管

# 3. 生成欧拉回路
euler_circuit = list(nx.eulerian_circuit(G, source=P))  # 从P出发的欧拉回路

# 4. 按maxLength拆解回路（示例：maxLength=20）
max_length = 20
current_length = 0
sub_circuits = []
current_circuit = [P]  # 每个子回路以P开头和结尾

for edge in euler_circuit:
    u, v, w = edge
    current_length += w
    current_circuit.append(v)
    if current_length >= max_length - 5:  # 预留5单位用于返回P的路径
        # 添加返回P的边（假设从v到P的最短距离可通过nx.shortest_path_length获取）
        return_length = nx.shortest_path_length(G, v, P, weight='weight')
        if current_length + return_length <= max_length:
            current_circuit.append(P)
            sub_circuits.append(current_circuit)
            current_circuit = [P]
            current_length = 0

print("拆解后的子回路：", sub_circuits)

三、总结与建议

• 最优方案优势：通过图论建模确保覆盖完整性，欧拉回路分解实现路径均衡，虚拟边处理灵活满足过路管约束，拐弯次数可通过图的边权重（如直角路径权重设为更高值）间接优化。
• 扩展优化：若需进一步控制管道间距，可在图边权重中加入间距惩罚项，或结合网格采样点生成路径点。

希望以上方案能帮到你！如果需要调整约束条件或补充细节，请随时留言。期待你的反馈，也请楼主采纳~