微分方程是
x(1-x)(550y-1000α+200)与y(1-y)(400x-200)
α=0.2,0.4,0.6,0.8,1. i=0.3 j=0.8 x∈[0,1]步长为0.1 t∈[0 0.06],求x与t的仿真图以及原始代码。
Matlab微分方程仿真图求解
- 写回答
- 好问题 0 提建议
- 关注问题
- 邀请回答
-
2条回答 默认 最新
 MatlabFans_Mfun 2021-07-27 21:44关注
MatlabFans_Mfun 2021-07-27 21:44关注我想题主的意思应该是求解下面的微分方程:
dx/dt = x(1-x)(550y-1000α+200)
dy/dt= y(1-y)(400x-200)
可使用ode45来求解这个常微分方程组,代码如下x0 = [0.3;0.8]; alpha = 0.2; dfun = @(t,X) [X(1)*(1-X(1))*(550*X(2)-1000*alpha+200); X(2)*(1-X(2))*(400*X(1)-200) ]; [T1,X1] = ode45( dfun,[0 0.06],x0); alpha = 0.4; dfun = @(t,X) [X(1)*(1-X(1))*(550*X(2)-1000*alpha+200); X(2)*(1-X(2))*(400*X(1)-200) ]; [T2,X2] = ode45( dfun,[0 0.06],x0); alpha = 0.6; dfun = @(t,X) [X(1)*(1-X(1))*(550*X(2)-1000*alpha+200); X(2)*(1-X(2))*(400*X(1)-200) ]; [T3,X3] = ode45( dfun,[0 0.06],x0); alpha = 0.8; dfun = @(t,X) [X(1)*(1-X(1))*(550*X(2)-1000*alpha+200); X(2)*(1-X(2))*(400*X(1)-200) ]; [T4,X4] = ode45( dfun,[0 0.06],x0); alpha = 1.0; dfun = @(t,X) [X(1)*(1-X(1))*(550*X(2)-1000*alpha+200); X(2)*(1-X(2))*(400*X(1)-200) ]; [T5,X5] = ode45( dfun,[0 0.06],x0); figure subplot(211) hold on plot(T1,X1(:,1)); plot(T2,X2(:,1)); plot(T3,X3(:,1)); plot(T4,X4(:,1)); plot(T5,X5(:,1)); xlabel('Time /s') ylabel('x') legend({'\alpha = 0.2','\alpha = 0.4','\alpha = 0.6','\alpha = 0.8','\alpha = 1.0'}) subplot(212) hold on plot(T1,X1(:,2)); plot(T2,X2(:,2)); plot(T3,X3(:,2)); plot(T4,X4(:,2)); plot(T5,X5(:,2)); xlabel('Time /s') ylabel('y') legend({'\alpha = 0.2','\alpha = 0.4','\alpha = 0.6','\alpha = 0.8','\alpha = 1.0'})结果图:
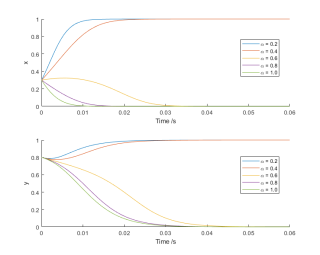 本回答被题主选为最佳回答 , 对您是否有帮助呢?解决 无用评论 打赏 举报
本回答被题主选为最佳回答 , 对您是否有帮助呢?解决 无用评论 打赏 举报
