cnn预测时间序列正确率低，预测曲线不波动

Question

问题遇到的现象和发生背景

cnn预测时间序列正确率低（0.1-0.3之间），预测曲线不波动（几乎为直线）
输入特征为 t-1 t-2 ...t-64 个时刻的 y, a, b,c, d. (y 与a,b, c, d, 相关，t时刻 y 与a,b, c, d, 相关性都在0.7-0.8)
输出特征为 t t+1 ...t+15 个时刻的y
Train on 10625 samples, validate on 800 samples

下图为训练集与验证集的损失函数与正确率

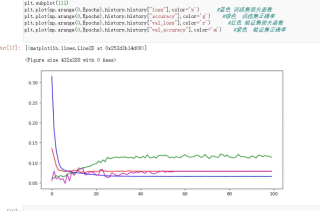
下图为测试集的实际输出与预测输出曲线

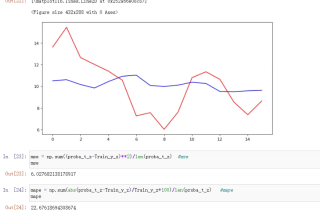
问题相关代码，请勿粘贴截图

网络代码

X21 = layers.Conv2D(filters=2,kernel_size=(5,2),padding="valid")(input1)  
X21 = layers.BatchNormalization(axis=-1, momentum=0.99, epsilon=0.001, center=True, scale=True, beta_initializer='zeros', gamma_initializer='ones', moving_mean_initializer='zeros', moving_variance_initializer='ones', beta_regularizer=None, gamma_regularizer=None, beta_constraint=None, gamma_constraint=None)(X21)
X21 = layers.Activation('relu')(X21)
X21 = layers.MaxPooling2D(pool_size=(2,1),padding="valid")(X21) 
X21 = layers.Dropout(0.5)(X21)
X21 = layers.Conv2D(filters=2,kernel_size=(3,1),padding="valid")(X21)  
X21 = layers.Activation('relu')(X21)
X21 = layers.MaxPooling2D(pool_size=(2,1),padding="valid")(X21)  
X21 = layers.Dropout(0.5)(X21)
X21 = layers.Conv2D(filters=32,kernel_size=(3,2),padding="valid")(X21)
X21 = layers.Flatten()(X21)
X21 = layers.Dense(32, activation='relu')(X21)
X21 = layers.Dropout(0.5)(X21)
X2 = layers.Dense(2*n1)(X21)

训练代码

model.compile(loss='mae',  optimizer=Adam(0.0001), metrics=['accuracy'])
  #ModelCheckpoint回调函数，在每个epoch后保存模型
  checkpoint = ModelCheckpoint(s,    monitor='val_loss',    verbose=0,    mode='auto',   period=1,   save_best_only=True)
  #ReduceLROnPlateau当检测指标未得到改善，进行n倍的学习率调整常常能获得较好的效果。
  plateau = ReduceLROnPlateau(monitor="val_loss",    verbose=0,  mode='auto',  factor=0.2,   patience=10,  epsilon=0.0001,    cooldown=0) 
  #Train_y_2d[xxa],Train_y_3d[xxa]是一样的
  history = model.fit([Train_x_2d_[xxa],Train_x_3d_[xxa]],Train_y_2d[xxa], epochs=Epochs, batch_size=256, shuffle=True,verbose=1,validat    ion_data=([Train_x_2d_[xxb],Train_x_3d_[xxb]],Train_y_2d[xxb]),callbacks=[checkpoint,plateau])

我的解答思路和尝试过的方法

都是无技巧的来回改动参数，如果有好的参数调整方向，请指教

改变优化器 损失函数 batch_size 学习率 epochs
改变卷积核大小 池化大小 加dropout层
改变验证集个数

请问 怎么能提高精度，减少误差。

Answer 1

（1）首先要考虑模型是否合理，也就是说能否以 t-1 t-2 ...t-64 个时刻的 y, a, b,c, d 预测 t t+1 ...t+15 个时刻的y
即使 t 时刻 y 与a,b, c, d, 相关性较高，也是不一定的。
例如，模型 y(t)= a x1(t)+b x2(t)+c x3(t)+d x4(t)，y(t) 与 x1~x4 的相关性理论上可以达到 100%，但 y(t) 与 y(t-1),..., xi(t-1),... 可以是完全无关的。

（2）如果你分析问题，认为 y(t) 与 y(t-1), ...y(t-k) 相关，且相关度较高，建议你先做一个模型，输入特征为 t-1 t-2 ...t-64 个时刻的 y, a, b,c, d，输出为 y(t)
也就是说先只做 一步预测，看看效果。如果这个模型都不好，说明问题不一定能用时序模型描述。
顺便说一句，如果 t 时刻 y 与a,b, c, d, 相关性都在0.7-0.8)，其实输入有没有 a,b,c,d 可能都差不多了，因为 y 与 abcd 高度相关。

（3）如果 yP(t) = F[ y(t-1), ...y(t-k) ] 的模型不错，你还是想预测更长的 yP(t+k)，首先预测性能下降是必然的。例如由历史和现有数据预测下一天的天气精度较高，预测时间越长则精度越低，甚至低的无法接受。
一个改进方法是，基于模型 yP(t) = F[ y(t-1), ...y(t-k) ]， 首先以 [ y(t-1), ...y(t-k) ] 预测得到 yP(t)，再以 [ yP(t), y(t-1)...y(t-k+1) ] 预测得到 yP(t+1)，依次类推.