A=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20];
x0=[8.5 0.26 0.21 16.2 0.074 41 197 0.998 3.02 0.5 9.8
5.8 0.24 0.44 3.5 0.029 5 109 0.9913 3.53 0.43 11.7
9.1 0.59 0.38 1.6 0.066 34 182 0.9968 3.23 0.38 8.5
7.1 0.32 0.32 11 0.038 16 66 0.9937 3.24 0.4 11.5
6.9 0.36 0.34 4.2 0.018 57 119 0.9898 3.28 0.36 12.7
6.6 0.36 0.29 1.6 0.021 24 85 0.98965 3.41 0.61 12.4
8.2 0.37 0.36 1 0.034 17 93 0.9906 3.04 0.32 11.7
8.2 0.37 0.36 1 0.034 17 93 0.9906 3.04 0.32 11.7
4.8 0.21 0.21 10.2 0.037 17 112 0.99324 3.66 0.48 12.2
4.8 0.17 0.28 2.9 0.03 22 111 0.9902 3.38 0.34 11.3
4.8 0.26 0.23 10.6 0.034 23 111 0.99274 3.46 0.28 11.5
4.8 0.13 0.32 1.2 0.042 40 98 0.9898 3.42 0.64 11.8
4.7 0.455 0.18 1.9 0.036 33 106 0.98746 3.21 0.83 14
4.4 0.54 0.09 5.1 0.038 52 97 0.99022 3.41 0.4 12.2
14.2 0.27 0.49 1.1 0.037 33 156 0.992 3.15 0.54 11.1
10.7 0.22 0.56 8.2 0.044 37 181 0.998 2.87 0.68 9.5
10.7 0.22 0.56 8.2 0.044 37 181 0.998 2.87 0.68 9.5
10 0.2 0.39 1.4 0.05 19 152 0.994 3 0.42 10.4
10 0.23 0.27 14.1 0.033 45 166 0.9988 2.72 0.43 9.7
9.9 0.49 0.23 2.4 0.087 19 115 0.9948 2.77 0.44 9.4
];
[n,m]=size(x0);
AGO=cumsum(A);
T=0;
x1=zeros(n,m+T);
for k=2:m
Z(k)=(AGO(k)+AGO(k+1))/2; %Z(i)为xi(1)的紧邻均值生成序列
end
for i=1:n
for j=1:m
for k=1:j
x1(i,j)=x1(i,j)+x0(i,k);%原始数据一次累加,得到xi(1)
end
end
end
x11=x1(:,1:m);
X=x1(:,1:m)';%截取矩阵
Yn =A;%Yn为常数项向量
Yn(1)=[]; %从第二个数开始,即x(2),x(3)...
Yn=Yn';
%Yn=A(:,2:m)';
B=[-Z',X];
C=(B'*B)(B'Yn);%由公式建立GM(1,n)模型
a=C(1);
b=C(:,2:n+1);
F=[];
F(1)=A(1);
u=zeros(1,m);
for i=1:m
for j=1:n
u(i)=u(i)+(b(j)x11(j,i));
end
end
for k=2:m
F(k)=(A(1)-u(k-1)/a)/exp(a(k-1))+u(k-1)/a;
end
G=[];
G(1)=A(1);
for k=2:m
G(k)=F(k)-F(k-1);%两者做差还原原序列,得到预测数据
end
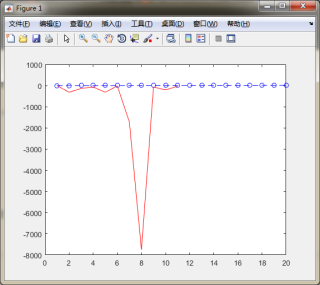
t1=0:m;
t2=0:m;
plot(t1,A,'bo--');
hold on;
plot(t2,G,'r-');