DAG演算法透過C++實踐

Question

Here is a Directed Acyclic Graph (DAG) with weight on nodes.

If there is a directed path from node to node , node is a successor of node . itself is defined as one of the successors of as well.
Please calculate the maximal weight among weights of all successors of for each in the DAG.

The first line is n,m , which are number of nodes and directed edges in the DAG.
The following n line are n integers representing weight of node , i0≤i<.
The following m line after weights are m pair of integers(a,b) , which represents directed edge from a to b .
Constraints
0<n<=10000
0<m<=50000
0<wieght<=10000
0<=a,b<n
Output Format
Print n integers in a line separate with a space.

The i-th integer is the answer corresponding to node i 0<=i<n
Sample Input
4 4
1 4 3 2
0 1
1 2
1 3
3 2
Sample Output
4 4 3 3
Sample Input
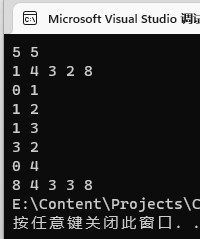
5 5
1 4 3 2 8
0 1
1 2
1 3
3 2
0 4
Sample Output
8 4 3 3 8

請問如何解？

#include <cstdio> 
#include <vector> 
#include <iostream>
 #include <algorithm> 
using namespace std;
int main() {
/* Enter your code here. Read input from STDIN. Print output to STDOUT */ 
return 0;
｝

Answer 1

#include <cstdio> 
#include <vector> 
#include <iostream>
#include <algorithm> 
using namespace std;
struct Node
{
    int weight;
    std::vector<int> successors;
};
int main() {
    int n, m;
    cin >> n >> m;
    std::vector<Node> nodes;
    nodes.resize(n);
    for (int i = 0; i < n; ++i)
    {
        int w;
        cin >> w;
        nodes[i].weight = w;
    }
    for (int i = 0; i < m; ++i)
    {
        int l, r;
        cin >> l >> r;
        nodes[l].successors.push_back(r);
    }
    for (int i = 0; i < n; ++i)
    {
        int maxWeight = nodes[i].weight;
        for (int j = 0; j < nodes[i].successors.size(); ++j)
        {
            if (maxWeight < nodes[nodes[i].successors[j]].weight)
            {
                maxWeight = nodes[nodes[i].successors[j]].weight;
            }
        }
        cout << maxWeight;
        if (i != n - 1)cout << " ";
    }
    return 0;
}