用matlab解决微积分的问题

Question

请记住使用完整的句子并解释你所有的答案。你可以在最多3人的小组中工作。最终的文档必须包含组中每个人的名字。你需要提交一个 Word文档(.doc)，以及一个MATLAB代码文件(.mlx)。

在这里，我们将开始使用MATLAB进行计算。你必须分析写出的问题，决定如何将问题写成积分的策略，讨论与积分有关的任何问题，实现一个或多个数值逼近的解决方案，然后讨论计算的潜在错误，

记住两个重要的规则:你不仅要解释你在做什么，还要解释你为什么这么做。论文必须有一个叙述结构;不要简单地写下每个问题并给出答案。这意味着你必须使用完整的句子。

对每一个积分都使用梯形和辛普森法则。你要决定除法的个数，足够让你相信你已经接近正确答案了。

Answer 1

基于Monster 组和GPT的调写：

%第一个公式
% 梯形法
n = 10; % 分割数
h = 2/n;
x = linspace(-1, 1, n+1);
y = -1./log(x);
I_trapezoidal = h/2 * (y(1) + 2*sum(y(2:n)) + y(n+1));
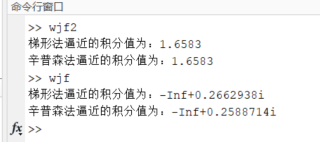
disp(['梯形法逼近的积分值为：', num2str(I_trapezoidal)])
% 辛普森法
n = 10; % 分割数
h = 2/n;
x = linspace(-1, 1, n+1);
y = -1./log(x);
I_simpson = h/3 * (y(1) + 4*sum(y(2:2:n)) + 2*sum(y(3:2:n-1)) + y(n+1));
disp(['辛普森法逼近的积分值为：', num2str(I_simpson)])

%第二个公式
% 梯形法
n = 1000; % 分割数
h = 10/n;
x = linspace(eps, 10, n+1); % 在0处添加微小的正数eps
y = sin(x)./x;
I_trapezoidal = h/2 * (y(1) + 2*sum(y(2:n)) + y(n+1));
disp(['梯形法逼近的积分值为：', num2str(I_trapezoidal)])
% 辛普森法
n = 1000; % 分割数
h = 10/n;
x = linspace(eps, 10, n+1); % 在0处添加微小的正数eps
y = sin(x)./x;
I_simpson = h/3 * (y(1) + 4*sum(y(2:2:n)) + 2*sum(y(3:2:n-1)) + y(n+1));
disp(['辛普森法逼近的积分值为：', num2str(I_simpson)])