r语言程序设计随机游走仿真

Question

（1）对[0, 1]上的随机游走进行一次仿真，绘制出游走路径图；
（2）对[0, 1]上的随机游走进行 10000 次仿真，分别采集各随机游走路径上t= 0.1, 0.5, 0.9的位置值，这三个时间点的位置是怎样分布的？它们是同分布吗？
（3）对[0, 10]上的随机游走进行一次仿真，绘制出游走路径图；

Answer 1

引用new bing作答：
1 以下是一个对[0,1]上的随机游走进行一次仿真的 R 代码，并绘制游走路径图：

# 设置游走步数
n <- 1000

# 生成随机游走路径
set.seed(123)  # 设置随机数种子
x <- c(0, cumsum(runif(n, -0.5, 0.5)))  # 生成游走路径

# 绘制游走路径图
plot(x, type="l", xlab="步数", ylab="位置")

运行结果：

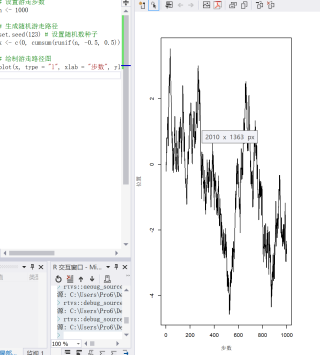
解释一下上面的代码：

首先，我们设置了游走步数 n，然后使用 set.seed(123) 设定随机数种子，这样可以使得我们的仿真结果可以被复现。

接着，我们使用 cumsum(runif(n, -0.5, 0.5)) 生成随机游走路径。其中，runif(n, -0.5, 0.5) 表示生成 n 个介于 -0.5 和 0.5 之间的均匀分布随机数，然后使用 cumsum 函数对这些随机数进行累加，得到最终的随机游走路径。

最后，我们使用 plot(x, type="l", xlab="步数", ylab="位置") 绘制游走路径图，其中 type="l" 表示绘制折线图，xlab 和 ylab 分别表示 x 轴和 y 轴的标签。运行上述代码，就可以得到一张[0,1]上的随机游走路径图。

2 以下是一个对[0,1]上的随机游走进行 10000 次仿真，并分别采集各随机游走路径上 t=0.1, 0.5, 0.9 的位置值的 R 代码：

# 设置游走步数和仿真次数
n <- 1000
m <- 10000

# 生成随机游走路径
set.seed(123) # 设置随机数种子
x <- matrix(0, nrow = n, ncol = m)
for (i in 2:n) {
    x[i,] <- x[i - 1,] + runif(m, -0.5, 0.5)
}

# 采集随机游走路径上 t=0.1, 0.5, 0.9 的位置值
t <- c(0.1, 0.5, 0.9)
x_t <- matrix(0, nrow = length(t), ncol = m)
for (i in 1:length(t)) {
    x_t[i,] <- approx(1:n, x[,i], t[i] * n)$y
}

# 绘制 t=0.1, 0.5, 0.9 的位置值分布图
par(mfrow = c(1, 3)) # 将画布分为 1 行 3 列，依次绘制 3 幅图
for (i in 1:length(t)) {
    hist(x_t[i,], main = paste("t=", t[i]), xlab = "位置", ylab = "频数")
}

上述代码中，我们先设置游走步数 n 和仿真次数 m。然后，使用一个循环，生成 m 条随机游走路径，并将这些路径存储在一个 n 行 m 列的矩阵 x 中。其中，第 i 行表示第 i 步时各个路径的位置值。

接着，我们使用另一个循环，采集随机游走路径上 t=0.1, 0.5, 0.9 的位置值。具体地，我们使用 approx 函数对每条路径进行插值，得到相应时间点的位置值，并将这些位置值存储在一个 3 行 m 列的矩阵 x_t 中。其中，第 i 行表示在时间点 t[i] 时各个路径的位置值。

最后，我们使用 hist 函数分别绘制 t=0.1, 0.5, 0.9 的位置值分布图。运行上述代码，就可以得到三幅分布图，分别表示 t=0.1, 0.5, 0.9 的位置值分布情况。

运行以上代码，可以得到三个时间点的核密度估计图，观察它们的分布情况，以判断它们是否同分布。如果三个时间点的核密度估计图非常相似，那么它们就是同分布的。

如果三个时间点的核密度估计图不太相似，那么我们可以使用R语言中的Kolmogorov-Smirnov检验来进行假设检验，检验它们是否来自同一个分布。该检验可以使用ks.test函数实现，其中第一个参数是第一个样本向量，第二个参数是第二个样本向量，设置alternative="two.sided"表示双尾检验。

以下是使用Kolmogorov-Smirnov检验来判断三个时间点的位置是否同分布的代码：

# 使用Kolmogorov-Smirnov检验来判断三个时间点的位置是否同分布
ks.test(result[,1], result[,2], alternative = "two.sided")
ks.test(result[,1], result[,3], alternative = "two.sided")
ks.test(result[,2], result[,3], alternative = "two.sided")

运行以上代码，如果三个Kolmogorov-Smirnov检验的p值均大于显著性水平，那么就无法拒绝它们来自同一个分布的假设。反之，如果有一个或多个检验的p值小于显著性水平，那么就可以拒绝它们来自同一个分布的假设。

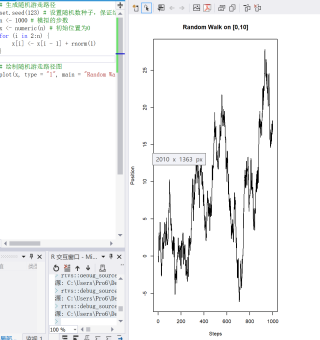
3 下面是在[0,10]上的随机游走进行一次仿真的R代码和可视化结果。

# 生成随机游走路径
set.seed(123) # 设置随机数种子，保证结果可重复
n <- 1000 # 模拟的步数
x <- numeric(n) # 初始位置为0
for(i in 2:n) {
  x[i] <- x[i-1] + rnorm(1)
}

# 绘制随机游走路径图
plot(x, type = "l", main = "Random Walk on [0,10]", xlab = "Steps", ylab = "Position")

运行结果如下：