有没有什么办法能够在这条离散的曲线上均匀的选取若干点?这条曲线是由3731个点构成的,我想从这3731个点中均匀的选取65个点,是沿这条曲线均匀地选取若干个点。是不是可以用测地线距离?
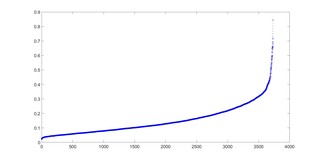
有没有什么办法能够在这条离散的曲线上均匀的选取若干点?这条曲线是由3731个点构成的,我想从这3731个点中均匀的选取65个点,是沿这条曲线均匀地选取若干个点。是不是可以用测地线距离?

 关注
关注引自强大而免费的微信小程序:皆我百晓生。
问题理解:
我们需要在给定的离散曲线上均匀选取若干点。具体来说,我们希望选取的点分布均匀,使得曲线上任意两个相邻点之间的距离尽可能相等。
解决思路:
一种常见的方法是使用插值算法来均匀选取若干点。具体步骤如下:
下面我们将详细介绍三种常见的插值算法:线性插值、多项式插值和样条插值。
1. 线性插值
线性插值方法是一种简单的插值方法,可以使用两个已知数据点之间的直线来估计中间的数值。对于一条曲线上的离散数据点(xi, yi),我们可以使用以下公式对两个连续点之间的插值点进行计算:
x = x1 + (x2 - x1) * t
y = y1 + (y2 - y1) * t
其中,x和y是插值点的坐标,t是一个介于0和1之间的权重参数。(x1, y1)和(x2, y2)是已知的数据点。
这样的插值算法可以在曲线上以等间距或者等时间间隔选择点。下面是一个使用线性插值算法选取若干点并将结果绘制成图形的示例代码:
import numpy as np
import matplotlib.pyplot as plt
def linear_interpolation(x, y, num_points):
new_x = []
new_y = []
for i in range(len(x)-1):
for j in range(num_points):
t = j / (num_points-1)
new_x.append(x[i] + (x[i+1] - x[i]) * t)
new_y.append(y[i] + (y[i+1] - y[i]) * t)
return new_x, new_y
# 假设有一条离散曲线的数据点
x = [0, 1, 2, 3, 4]
y = [0, 2, 1, 3, 2]
# 使用线性插值算法选取10个插值点
num_points = 10
new_x, new_y = linear_interpolation(x, y, num_points)
# 绘制离散曲线和插值点
plt.scatter(x, y, label='原始数据')
plt.scatter(new_x, new_y, color='r', marker='x', label='插值点')
plt.plot(x, y, label='离散曲线')
plt.plot(new_x, new_y, '--', label='插值曲线')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
代码中使用linear_interpolation函数实现了线性插值算法,可以根据给定的原始数据点和插值点的数量生成插值后的坐标,并绘制出离散曲线和插值曲线的图形。
2. 多项式插值
多项式插值方法通过拟合一条多项式曲线,使用已知的数据点去估计曲线上的其他点。具体来说,我们可以通过Lagrange插值多项式或Newton插值多项式来实现多项式插值算法。
这里我们以Lagrange插值多项式为例,通过给定的数据点(xi, yi),我们可以使用以下公式计算Lagrange插值多项式的值:
L(x) = y1 * l0(x) + y2 * l1(x) + ... + yn * ln(x)
其中l0(x), l1(x), ..., ln(x)是Lagrange插值多项式的基础多项式,可以通过以下公式计算:
li(x) = (x - x0)(x - x1)...(x - xi-1)(x - xi+1)...(x - xn) / (xi - x0)(xi - x1)...(xi - xi-1)(xi - xi+1)...(xi - xn)
将上述计算公式应用于多个数据点,可以得到一条独特的多项式曲线,我们可以使用这个曲线来进行插值。
以下是一个使用多项式插值算法选取若干点并将结果绘制成图形的示例代码:
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import lagrange
# 假设有一条离散曲线的数据点
x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 2, 1, 3, 2])
# 使用Lagrange插值方法拟合多项式
poly = lagrange(x, y)
# 生成插值点
num_points = 10
new_x = np.linspace(x[0], x[-1], num_points)
new_y = poly(new_x)
# 绘制离散曲线和插值点
plt.scatter(x, y, label='原始数据')
plt.scatter(new_x, new_y, color='r', marker='x', label='插值点')
plt.plot(x, y, label='离散曲线')
plt.plot(new_x, new_y, '--', label='插值曲线')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
上述代码使用scipy库的lagrange函数来实现Lagrange插值方法,通过给定的离散数据点进行拟合,并生成插值点的坐标。最后使用matplotlib库将离散曲线和插值曲线绘制成图形。
3. 样条插值
样条插值方法通过连接多个小段的曲线来估计整个曲线。具体来说,我们可以将曲线分割成多个小段,每个小段都是一个低次数的多项式曲线,我们可以通过拟合这些小段曲线来实现插值。
其中,一种常见的样条插值算法是基于三次多项式的插值算法(Cubic Spline Interpolation)。这种算法将整个曲线分割成多个小段,每个小段都是一个三次多项式。在每个小段内,我们可以使用已知的数据点来确定多项式的系数,然后利用这些系数来计算其余点的值。
以下是一个使用样条插值算法选取若干点并将结果绘制成图形的示例代码:
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CubicSpline
# 假设有一条离散曲线的数据点
x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 2, 1, 3, 2])
# 使用三次样条插值算法进行插值
cs = CubicSpline(x, y)
# 生成插值点
num_points = 10
new_x = np.linspace(x[0], x[-1], num_points)
new_y = cs(new_x)
# 绘制离散曲线和插值点
plt.scatter(x, y, label='原始数据')
plt.scatter(new_x, new_y, color='r', marker='x', label='插值点')
plt.plot(x, y, label='离散曲线')
plt.plot(new_x, new_y, '--', label='插值曲线')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
上述代码使用scipy库的CubicSpline函数来实现基于三次样条插值算法,通过给定的离散数据点进行拟合,并生成插值点的坐标。最后使用matplotlib库将离散曲线和插值曲线绘制成图形。
以上就是使用插值算法在离散曲线上均匀选取若干点的方法。根据实际需求选择合适的插值方法,并根据需要调整插值点的数量,即可得到均匀分布的插值点。