Problem Description
Engineer Bob is a strange man, and he makes his floor a simple polygon and installs various fantastic machines on his floor.
On Bob’s floor, there are n machines and n sockets. Each machine is fixed at a certain location and each socket is fixed at a certain position. Different machines and socket may be located at the same position.
Bob wants to connect one machine with exactly one socket by using wire and he hopes that the total length of the wires is minimal.
In addition, we assume that:
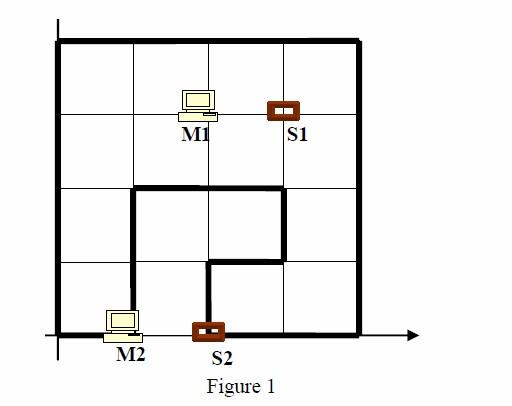
Bob’s floor can be described by m vertices in a 2-dimentional coordinate system. The m vertices are always given by clockwise or counter-clockwise. For simplicity, the edges of the polygon are always horizontal or vertical. For example, (0,0) (0,4) (4,4) (4,0) (2,0) (2,1) (3, 1) (3,2) (1,2) (1,0) describe the polygon which is shown in Figure 1, in which M1 and M2 are machines, S1 and S2 are sockets.
Wires can only be equipped within the polygon or on the edges of the polygon. Wires can be intercrossed.
Now please find out the minimal length of all the wires needed.
Input
The input contains several cases. The first line of each case contains one integer m (1 ≤ m ≤ 100) indicating the number of vertices of the polygon. This is then followed by m lines, in which the ith line contains two integers x (0 ≤ x ≤ 10,000) and y (0 ≤ y ≤ 10,000), indicating the coordinate of the ith vertex of the polygon. And this is followed by one line, containing one integer n (1 ≤ n ≤ 16), indicating the number of machines (and also sockets).
This is followed by n lines, in which the ith line contains two integers x (0 ≤ x ≤ 10,000) and y (0 ≤ y ≤ 10,000), indicating the coordinate of the ith machine. And this is followed by n lines, in which the ith line contains two integers x (0 ≤ x ≤ 10,000) and y (0 ≤ y ≤ 10,000), indicating the coordinate of the ith socket. The input ends with m=0. It is guaranteed that the coordinates of all machines and sockets are always given within the polygon or on the edges of the polygon.
Output
For each case, output a floating-point number to two decimal places, indicating the minimal length of wires needed.
Sample Input
10
0 0
0 4
4 4
4 0
2 0
2 1
3 1
3 2
1 2
1 0
2
2 3
1 0
3 3
2 0
0
Sample Output
7.41