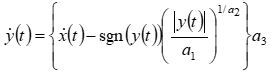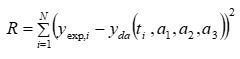Matlab 非线性最小二乘法 求解微分方程

Question

如下微分方程，求解微分方程系数（a1, a2, a3）

1）没有dx/dt 的方程
2）yexp是实验值
3）先假定a1,a2,a3，应用ode45计算解析值y,然后用lsqcurvefit求系数

代码如下：

t = data(:,1);
x = data(:,2);
y_exp = data(:,3);

dt = t(2) - t(1);
len = length(x);
dx_dt(1) = x(1)/dt;
dx_dt(2:len) = diff(x) / dt;
dy_exp(1) = y_exp(1)/dt;
dy_exp(2:len) = diff(y_exp) / dt;

a1 = 10.74;
a2 = 0.91;
a3 = 290;

get_dx_dt = @(t_sim) interp1(t(1:end), dx_dt, t_sim);
dy_dt = @(t,y)(get_dx_dt(t)-sign(y)*(abs(y)/a1)^(1/a2))*a3;
[tout, y] = ode4(dy_dt, t(1), dt, t(end), y_exp(1));

len_y = length(y);
x1 = dx_dt(1:len_y);
x2 = y';
Y =dy_exp(1:len_y);
X=[x1;x2]';
a0=rand(1,3);
func=@(a,X)(x1-sign(x2).*(abs(x2)/a(1)).^(1/a(2)))*a(3);
a=lsqcurvefit(func,a0,X,Y);

计算得到的a为复数。
请问:
1.思路是否正确；
2.如果思路不正确，能否指明正确思路

谢谢

Answer 1

你好，既然你知道了y和x那么数值求到了dy/dt和dx/dt，自然就可以通过插值方法得到与x和y等长的dy/dt和dx/dt，然后直接进行拟合就好了啊，lsqcurvefit也好，最小二乘法加上fminsearch求解也罢，都可以做啊！