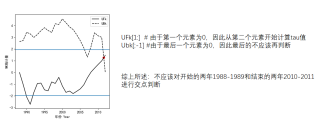
背景:python对时间序列栅格数据进行mann-kendall突变检测
问题:同一组数据,为什么无论如何改变时间长短,突变点在第一年和倒数第二年的像元是最多的?
(例如:检测1988-2010年,则1988和2009年突变的像元最多;检测1999-2005年,则1999年和2004年突变的像元最多)
第一年突变的像元和倒数第二年突变的像元是否有意义?是什么意义?是公式的问题吗?能否直接去掉?
结果:
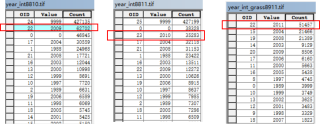
相关代码:
#用于输出突变点位置(x坐标,即突变年份)的代码
def judge_points(x, y):
pointx = [0]
pointy = [0]
time = list(range(1988, 2011))
# print("time:", time)
n = len(time)
for i in range(n):
if i < n - 1:
# print("time[%s]:"%i,time[i])
x1 = float(time[i]) # 取四点坐标
y1 = float(x[i])
x2 = float(time[i + 1])
y2 = float(x[i + 1])
x3 = float(time[i])
y3 = float(y[i])
x4 = float(time[i + 1])
y4 = float(y[i + 1])
# print("输入:", y1, y2, y3, y4)
k1 = (y2 - y1) / (x2 - x1) # 计算k1,由于点均为整数,需要进行浮点数转化
k2 = (y4 - y3) / (x4 - x3) # 斜率存在操作
b1 = y1 - x1 * k1 # 整型转浮点型是关键
b2 = y3 - x3 * k2
if (k1-k2)!=0:
x0 = (b2 - b1) / (k1 - k2)
else: x0=0
y0 = k1 * x0 + b1
if -1.96 < y0 < 1.96 and time[i] < x0 < time[i + 1]:
pointx.append(x0)
pointy.append(y0)
# print("pointx:", pointx)
# print("pointy:", pointy)
pointx[0] = 1
if pointx[0] == 1:
# print("有")
return pointx[1], pointy[1]
else:
# print("没有")
return 0, 0
#mk突变检验的实现方法
def mktest(inputdata):
inputdata = np.array(inputdata)
n = inputdata.shape[0]
Sk = [0]
UFk = [0]
s = 0
Exp_value = [0]
Var_value = [0]
for i in range(1, n):
for j in range(i):
if inputdata[i] > inputdata[j]:
s = s + 1
else:
s = s + 0
Sk.append(s)
Exp_value.append((i + 1) * (i + 2) / 4)
Var_value.append((i + 1) * i * (2 * (i + 1) + 5) / 72)
UFk.append((Sk[i] - Exp_value[i]) / np.sqrt(Var_value[i]))
Sk2 = [0]
UBk = [0]
UBk2 = [0]
s2 = 0
Exp_value2 = [0]
Var_value2 = [0]
inputdataT = list(reversed(inputdata))
for i in range(1, n):
for j in range(i):
if inputdataT[i] > inputdataT[j]:
s2 = s2 + 1
else:
s2 = s2 + 0
Sk2.append(s2)
Exp_value2.append((i + 1) * (i + 2) / 4)
Var_value2.append((i + 1) * i * (2 * (i + 1) + 5) / 72)
UBk.append((Sk2[i] - Exp_value2[i]) / np.sqrt(Var_value2[i]))
UBk2.append(-UBk[i])
UBkT = list(reversed(UBk2))
return UFk, UBkT