请问如何用python结合遗传算法和多目标优化计算得出最佳结果？

代码

from random import randint as rd

fc=20 #父代数量
equipment=[["knife",10,1],["Beans",20,5],["Potatoes",15,10],["Onions",2,1],["Sleeping Bag",30,7],["Rope",10,5],["Compass",30,1]]
fathers=[]  #父代，每个父代7个基因位(因为一共7个物品)。
maxValue=0 #最高得分
maxSon=[]

def makeFathers(fathers): #产生初始父代
    for i in range(fc):
        father=[]
        for j in range(7):
            gen=rd(0,6) #随即生成父代基因位
            if gen in father: #如果该基因已存在
                father.append(7) #则添加一个7号基因（即不存在，表示此位置不带物品）
            else:
                father.append(gen) #否则添加该随即基因
        fathers.append(father)

def makeSons(sons): #交配（父代基因交换）
    sons.clear()
    for i in range(fc-1):
        for j in range(fc-1-i):
            son=fathers[i].copy()
            son[4:]=fathers[i+j+1][4:]
            sons.append(son)

def exchange(sons): #等位交换
    for i in sons:
        if rd(0,10)>8: #概率发生
            g1=rd(0,6) #发生交换的基因位1
            g2=rd(0,6) #发生交换的基因位2
            i[g1],i[g2]=i[g2],i[g1]

def change(sons): #突变
    for i in sons:
        if rd(0,10)>8: #概率发生
            i[rd(0,6)]=rd(0,7) #随即一位的基因变为随机

def kill(sons): #杀死不符合的子代
    sonsTmp=[]
    for i in sons:
        son=i.copy()
        son.sort()
        flag=0 #基因重复标记
        weight=0 #重量计数
        for j in range(6):
            if son[j]==son[j+1] and son[j]!=7:
                flag+=1
            if son[j]!=7:
                weight+=equipment[son[j]][2] #基因位重量累加
        if son[6]!=7:
            weight+=equipment[son[6]][2]
        if not (flag>0 or weight>20): #如果不出现重复或超重
            sonsTmp.append(i)
    sons.clear()
    for i in sonsTmp:
        sons.append(i)

def rank(sons): #子代评分
    global maxValue
    global maxSon
    values=[]
    for i in sons:
        value=0 #初始评分
        for j in range(7):
            if i[j]!=7:
                value+=equipment[i[j]][1] #物品得分累加
        if value>120:
            print(i)
        i.append(value) #为子代添加评分
        values.append(value) #为总评分列表添加评分
    values.sort() #评分排序
    if maxValue<values[-1]:
        maxValue=values[-1]
    sonsTmp=[]
    for i in sons:  #将评分低于第20高得分的子代杀死
        if i[-1]>values[-fc]:
            sonsTmp.append(i)
        if i[-1]==maxValue:
            maxSon=i[:-1].copy()
    print("本轮最高得分 :%d ,目前最佳得分 :%d" % (values[-1],maxValue))
    print(maxSon)
    fathers=sonsTmp.copy() #剩余子代作为新父代

def main():
    sons=[]
    makeFathers(fathers)
    for i in range(100):  #100次迭代
        makeSons(sons)
        exchange(sons)
        change(sons)
        kill(sons)
        rank(sons)

main()

运行结果

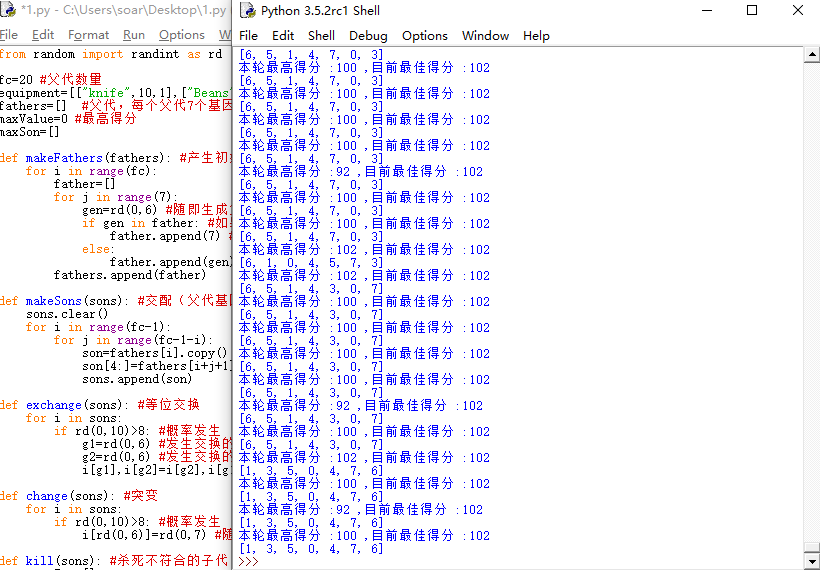
实际上102就是最佳值，因为样本小，好多时候一上来就是最佳值。