__夏殇__ 2021-08-23 21:15 采纳率: 100%
浏览 1039
已结题

matlab 求解含有三角函数的多变量方程组

img

  • 写回答

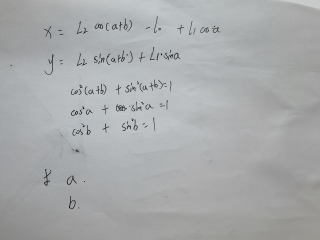
1条回答 默认 最新

  • joel_1993 2021-08-23 21:27
    关注

    你好，利用matlab的符号工具箱，可以解出a和b，有两对解：

    syms x y L1 L2 L0 a b
eq = [x-L2*cos(a+b)+L0-L1*cos(a);
    y - L2*sin(a+b) - L1*sin(a)];
[a,b] = solve(eq, [a,b])

    解的结果为

    a =
 
 2*atan((((8*L1^2*L2*y)/((L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2)*(L0^2 + 2*L0*L1 + 2*L0*x + L1^2 + 2*L1*x - L2^2 + x^2 + y^2)) + (4*L1*L2*(-(L0^2 + 2*L0*x - L1^2 - 2*L1*L2 - L2^2 + x^2 + y^2)*(L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2))^(1/2))/((L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2)*(L0^2 + 2*L0*L1 + 2*L0*x + L1^2 + 2*L1*x - L2^2 + x^2 + y^2)))*(L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2))/(4*L1*L2))
 2*atan((((8*L1^2*L2*y)/((L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2)*(L0^2 + 2*L0*L1 + 2*L0*x + L1^2 + 2*L1*x - L2^2 + x^2 + y^2)) - (4*L1*L2*(-(L0^2 + 2*L0*x - L1^2 - 2*L1*L2 - L2^2 + x^2 + y^2)*(L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2))^(1/2))/((L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2)*(L0^2 + 2*L0*L1 + 2*L0*x + L1^2 + 2*L1*x - L2^2 + x^2 + y^2)))*(L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2))/(4*L1*L2))
 
 
b =
 
 -2*atan((-(L0^2 + 2*L0*x - L1^2 - 2*L1*L2 - L2^2 + x^2 + y^2)*(L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2))^(1/2)/(L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2))
  2*atan((-(L0^2 + 2*L0*x - L1^2 - 2*L1*L2 - L2^2 + x^2 + y^2)*(L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2))^(1/2)/(L0^2 + 2*L0*x - L1^2 + 2*L1*L2 - L2^2 + x^2 + y^2))

    用公式打印可以得到解的具体表达式

    img

    本回答被题主选为最佳回答 , 对您是否有帮助呢?
    评论

报告相同问题？

问题事件

  • 系统已结题 10月28日
  • 已采纳回答 10月20日
  • 创建了问题 8月23日

悬赏问题

  • ¥100 set_link_state
  • ¥15 虚幻5 UE美术毛发渲染
  • ¥15 CVRP 图论 物流运输优化
  • ¥15 Tableau online 嵌入ppt失败
  • ¥100 支付宝网页转账系统不识别账号
  • ¥15 基于单片机的靶位控制系统
  • ¥15 真我手机蓝牙传输进度消息被关闭了，怎么打开？(关键词-消息通知)
  • ¥15 装 pytorch 的时候出了好多问题，遇到这种情况怎么处理？
  • ¥20 IOS游览器某宝手机网页版自动立即购买JavaScript脚本
  • ¥15 手机接入宽带网线，如何释放宽带全部速度