数值分析实验 用matlab(任何语言都可)

Question

给出代码和结果截图

Answer 1

你好同学，代码供参考，答题不易，如有帮助还望给个宝贵的采纳支持一下答主答题哟，非常感谢
第一题

% 第一题：
I0 = log(1.2); % 初始值,当n=0时，I0=log(6)-log(5)=log(1.2)
for n = 1:30 % 迭代30次
   I =  1/n - 5*I0;
   fprintf('n=%d时，I%d=%f\n',n, n, I);
   I0 = I;
end

第一题结果：

n=1时，I1=0.088392
n=2时，I2=0.058039
n=3时，I3=0.043139
n=4时，I4=0.034306
n=5时，I5=0.028468
n=6时，I6=0.024325
n=7时，I7=0.021233
n=8时，I8=0.018837
n=9时，I9=0.016926
n=10时，I10=0.015368
n=11时，I11=0.014071
n=12时，I12=0.012977
n=13时，I13=0.012040
n=14时，I14=0.011229
n=15时，I15=0.010522
n=16时，I16=0.009890
n=17时，I17=0.009372
n=18时，I18=0.008696
n=19时，I19=0.009151
n=20时，I20=0.004243
n=21时，I21=0.026406
n=22时，I22=-0.086575
n=23时，I23=0.476352
n=24时，I24=-2.340094
n=25时，I25=11.740469
n=26时，I26=-58.663883
n=27时，I27=293.356454
n=28时，I28=-1466.746558
n=29时，I29=7333.767272
n=30时，I30=-36668.803026

可见当n=24的时候积分已经出现了负值了

第二题
牛顿迭代法计算根号7，原理
要计算根号7，首先要构造函数f=x^2-7，即计算函数f=0时的x的值，这个时候用牛顿迭代法xn+1=xn-f(xn)/f'(xn)：

f=@(x) x^2-7;
df = @(x) 2*x; % f的导数f'
err = 1;%误差初始值
x = 2;%迭代初始值
count = 0; % 迭代次数计步
while (err>5e-15)%如果没收敛就继续迭代
    count = count + 1;
    dx = f(x)/df(x);
    x = x - dx;
    err = abs(dx);
    N = -floor(log10(abs(x-sqrt(7))));
    fprintf('第%d次迭代, 误差为%e，x=%.16f\n', count, err, x);
end

第二题结果：

第1次迭代, 误差为7.500000e-01，x=2.7500000000000000
第2次迭代, 误差为1.022727e-01，x=2.6477272727272729
第3次迭代, 误差为1.975224e-03，x=2.6457520483808037
第4次迭代, 误差为7.373161e-07，x=2.6457513110646933
第5次迭代, 误差为1.027242e-13，x=2.6457513110645907
第6次迭代, 误差为1.678499e-16，x=2.6457513110645907

根据第六次迭代，可见第五次迭代，其有效数字已经满足了15位的要求了

第三题

% 这道题关键是怎么确定ek+1和ek的关系，根据收敛阶的定义
% 计算出p的大小
% 由于ek+1/ek^p=C
% 两边取对数，log(ek+1) = p*log(ek) + log(C)
% 所以斜率就是收敛阶
x0 = 0.1;
nstep = 20;
err_arr = zeros(nstep,1);
for i = 1:nstep
    x = 0.99*x0-x0^2;
    err = abs(x-x0);
    err_arr(i) = err;
    x0=x;
end
ek = err_arr(1:end-1); % ek
ek1 = err_arr(2:end); % ek+1
parr = polyfit(log(ek),log(ek1),1);
figure(1);clf
loglog(ek,ek1)
xlabel('log(e_k)')
ylabel('log(e_{k+1})')
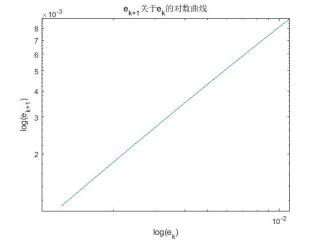
title('e_{k+1}关于e_k的对数曲线')
axis equal
p = parr(1);
fprintf('对数曲线斜率为%f,所以是%f阶收敛\n',p,p);

结果：

对数曲线斜率为0.935333,所以是0.935333阶收敛

收敛阶对数曲线图形